题目内容
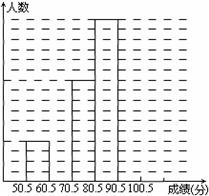 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
(Ⅱ)补全频数直方图;
(Ⅲ)学校决定成绩在75.5~85.5分的学生为二等奖,问该校获得二等奖的学生约为多少人?
分析:(1)根据样本容量,频率和频数之间的关系得到要求的几个数据,注意第三个数据是用样本容量减去其他三个数得到.
(2)首先根据表格中已知频率乘以总人数即可求出小组的频数,再根据所有频率之和为1可以求出最后一个未知小组的频率,然后乘以总人数就可以求出这组的频数,最后根据表格数据库补全频数分布直方图;
(3)先计算出成绩在76.5~85.5的学生频率为0.26,由于有900名学生参加了这次竞赛,所以该校获得二等奖的学生约为0.26×900=234(人).
(2)首先根据表格中已知频率乘以总人数即可求出小组的频数,再根据所有频率之和为1可以求出最后一个未知小组的频率,然后乘以总人数就可以求出这组的频数,最后根据表格数据库补全频数分布直方图;
(3)先计算出成绩在76.5~85.5的学生频率为0.26,由于有900名学生参加了这次竞赛,所以该校获得二等奖的学生约为0.26×900=234(人).
解答: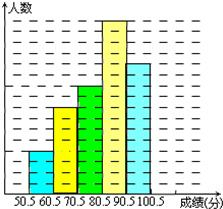 解:(1)
解:(1)
(4分)
(2)频数直方图如图所示(8分)
(3)成绩在75.5~80.(5分)的学生占70.5~80.5的学生的
,因为成绩在70.5~80.5的学生频率为0.2,所以成绩在75.5~80.5的学生频率为0.1,(10分)
成绩在80.5~85.5的学生占80.5~90.5的学生的
,因为成绩在80.5~90.5的学生频率为0.32,所以成绩在80.5~85.5的学生频率为0.16(12分)
所以成绩在76.5~85.5的学生频率为0.26,由于有900名学生参加了这次竞赛,所以该校获得二等奖的学生约为0.26×900=234(人)(14分)
 解:(1)
解:(1)| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | 12 | 0.24 |
| 合计 | 50 | 1.00 |
(2)频数直方图如图所示(8分)
(3)成绩在75.5~80.(5分)的学生占70.5~80.5的学生的
| 5 |
| 10 |
成绩在80.5~85.5的学生占80.5~90.5的学生的
| 5 |
| 10 |
所以成绩在76.5~85.5的学生频率为0.26,由于有900名学生参加了这次竞赛,所以该校获得二等奖的学生约为0.26×900=234(人)(14分)
点评:本小题主要考查频率分布直方图、用样本的频率分布估计总体分布等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
相关题目
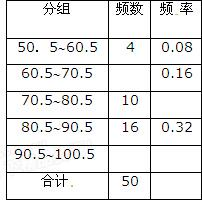
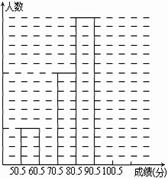 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛、为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计、则分数在60.5~70.5的学生有( )名
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛、为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计、则分数在60.5~70.5的学生有( )名
 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有1000名学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表和频数分布条形图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有1000名学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表和频数分布条形图,解答下列问题: