由题设与为的解．——青夏教育精英家教网—

已知椭圆x²＋＝1及两点P(－2，0)、Q(0，1)，过点P作斜率为k的直线交椭圆于不同的两点A、B，设线段AB的中点为M，连结QM．

(1)k为何值时，直线QM与椭圆的准线平行？

(2)试判断直线QM能否过椭圆的顶点？若能，求出相应的k值，若不能，说明理由．

解答题：解答应写出文字说明，证明过程或演算步骤．

已知椭圆的一个顶点为A(0，－1)，焦点在x轴上，若右焦点到直线x－y＋2＝0的距离为3．

(1)

求椭圆的标准方程

(2)

设直线l：y＝x＋m，是否存在实数m，使直线l与1中的椭圆有两个不同的交点M、N，且若存在，求出m的值；若不存在，请说明理由．

解答题

用水清洗一堆蔬菜上残留的农药．对用一定量的水清洗一次的效果作如下假定：用1个单位量的水可洗掉蔬菜上残留农药量的，用水越多洗掉的农药量也越多，但总还有农药残留在蔬菜上．设用x单位量的水清洗一次以后，蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x)．

(1)

试规定f(0)的值，并解释其实际意义；

(2)

试根据假定写出函数f(x)应该满足的条件和具有的性质；

(3)

解：设f(x)＝，现有a(a＞0)单位量的水，可以清洗一次，也可以把水平均分成2份后清洗两次，试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由．

解答题：解答应写出文字说明，证明过程或演算步骤．

设P(x₁，y₁)，Q(x₂，y₂)是抛物线C：y²＝2px(p＞0)上相异两点，且，直线PQ与x轴相交于E．

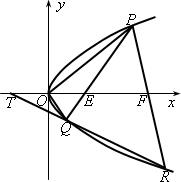
(Ⅰ)若P，Q到x轴的距离的积为4，求p的值；

(Ⅱ)若p为已知常数，在x轴上，是否存在异于E的一点F，使得直线PF与抛物线的另一交点为R，而直线RQ与x轴相交于T，且有，若存在，求出F点的坐标(用p表示)，若不存在，说明理由．

解答题

用水清洗一堆蔬菜上残留的农药．对用一定量的水清洗一次的效果作如下假定：用1个单位量的水可洗掉蔬菜上残留农药量的，用水越多洗掉的农药量也越多，但总还有农药残留在蔬菜上．设用x单位量的水清洗一次以后，蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x)．

(1)

试规定f(0)的值，并解释其实际意义；

(2)

试根据假定写出函数f(x)应该满足的条件和具有的性质；

(3)

解：设f(x)＝，现有a(a＞0)单位量的水，可以清洗一次，也可以把水平均分成2份后清洗两次，试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由．

试题分类