摘要:解:(1)由题意-----2分
网址:http://m.1010jiajiao.com/timu_id_28175[举报]
t∈R,t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).问:①直线PQ是否能通过下面的点M(6,1),N(4,5);②在△OPQ内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在边OP上.

(1)求证:顶点C一定在直线y=![]() x上.
x上.
(2)求下图中阴影部分面积的最大值,并求这时顶点A、B、C、D的坐标.
查看习题详情和答案>>.(本题满分13分)设函数 ,方程f(x)=x有唯一的解,
,方程f(x)=x有唯一的解,
已知f(xn)=xn+1(n∈N﹡)且f(xl)= .
.
(1)求证:数列{ )是等差数列;
)是等差数列;
(2)若 ,求Sn=b1+b2+b3+…+bn
,求Sn=b1+b2+b3+…+bn
(3)在(2)的条件下,是否存在最小正整数m,使得对任意n∈N﹡,有 成立,若存在,求出m的值;若不存在,请说明理由。
成立,若存在,求出m的值;若不存在,请说明理由。
查看习题详情和答案>>
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设二次函数![]() ,对任意实数
,对任意实数![]() ,
,![]() 恒成立;数列
恒成立;数列![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式和值域;
的解析式和值域;
(2)试写出一个区间![]() ,使得当
,使得当![]() 时,数列
时,数列![]() 在这个区间上是递增数列,
在这个区间上是递增数列,
并说明理由;
(3)已知![]() ,求:
,求: .
.
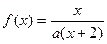 ,方程
,方程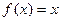 有唯一解,已知
有唯一解,已知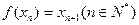 ,且
,且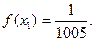
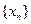 的通项公式;
的通项公式;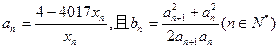 ,求和
,求和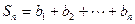 ;
;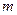 ,使得对任意
,使得对任意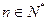 ,有
,有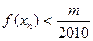 成立,若存在;求出
成立,若存在;求出