网址:http://m.1010jiajiao.com/timu_id_280414[举报]
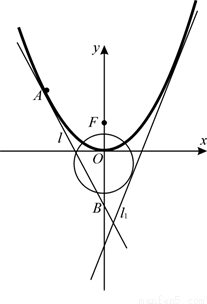
如图,已知直线 (
(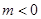 )与抛物线
)与抛物线 :
: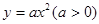 和圆
和圆 :
: 都相切,
都相切, 是
是 的焦点.
的焦点.
(Ⅰ)求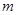 与
与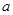 的值;
的值;
(Ⅱ)设 是
是 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点 ,以
,以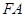 、
、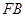 为邻边作平行四边形
为邻边作平行四边形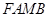 ,证明:点
,证明:点 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点 所在的定直线为
所在的定直线为 , 直线
, 直线 与
与 轴交点为
轴交点为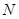 ,连接
,连接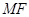 交抛物线
交抛物线 于
于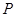 、
、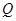 两点,求△
两点,求△ 的面积
的面积 的取值范围.
的取值范围.
【解析】第一问中利用圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去)
舍去)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
,
第二问中,由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形
, ∵四边形FAMB是以FA、FB为邻边作平行四边形
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线
第三问中,设直线 ,代入
,代入 得
得 结合韦达定理得到。
结合韦达定理得到。
解:(Ⅰ)由已知,圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去). …………………(2分)
舍去). …………………(2分)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
, .
……(2分)
.
……(2分)
(Ⅱ)由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形,
, ∵四边形FAMB是以FA、FB为邻边作平行四边形,
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线 上.…(2分)
上.…(2分)
(Ⅲ)设直线 ,代入
,代入 得
得 , ……)得
, ……)得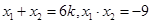 ,
…………………………… (2分)
,
…………………………… (2分)
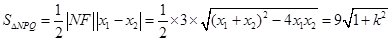 ,
,
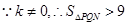 .
. △
△ 的面积
的面积 范围是
范围是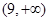
查看习题详情和答案>>
如图,三棱柱 中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。

(I) 证明:平面 ⊥平面
⊥平面
(Ⅱ)平面 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算,考查空间想象能力、逻辑推理能力,是简单题.
【解析】(Ⅰ)由题设知BC⊥ ,BC⊥AC,
,BC⊥AC, ,∴
,∴ 面
面 , 又∵
, 又∵
 面
面 ,∴
,∴ ,
,
由题设知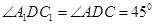 ,∴
,∴ =
= ,即
,即 ,
,
又∵ , ∴
, ∴ ⊥面
⊥面 , ∵
, ∵
 面
面 ,
,
∴面 ⊥面
⊥面 ;
;
(Ⅱ)设棱锥 的体积为
的体积为 ,
, =1,由题意得,
=1,由题意得, =
= =
= ,
,
由三棱柱 的体积
的体积 =1,
=1,
∴ =1:1, ∴平面
=1:1, ∴平面 分此棱柱为两部分体积之比为1:1
分此棱柱为两部分体积之比为1:1
查看习题详情和答案>>
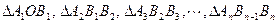 均为等腰直角三角形, 已知它们的直角顶点
均为等腰直角三角形, 已知它们的直角顶点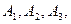 …,
…,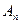 在曲线
在曲线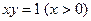 上,
上,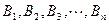 在
在 轴上(如图),
轴上(如图),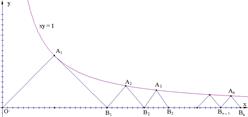
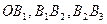 的长;
的长;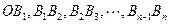 的通项公式.
的通项公式.