摘要:9分(3)设取出3球中颜色都不相同的事件为B.则有
网址:http://m.1010jiajiao.com/timu_id_27607[举报]
暗箱中开始有3个红球,2个白球.每次从暗箱中取出一球后,将此球以及与它同色的5个球(共六个球)一齐放回暗箱中.
(1)求第二次取出红球的概率
(2)求第三次取出白球的概率;
(3)设取出白球得5分,取出红球得8分,求连续取球3次得分的期望值. 查看习题详情和答案>>
(1)求第二次取出红球的概率
(2)求第三次取出白球的概率;
(3)设取出白球得5分,取出红球得8分,求连续取球3次得分的期望值. 查看习题详情和答案>>
已知暗箱中开始有3个红球,2个白裘。现每次从暗箱中取出一个球后,再将此球以及与它同色的5个球(共6个球)一起放回箱中。
(1)求第二次取出红球的概率;
(2)求第三次取出白球的概率;
(3)设取出白球得5分,取出红球得8分,求连续取球3次得分的期望值。
查看习题详情和答案>>已知暗箱中开始有3个红球,2个白裘。现每次从暗箱中取出一个球后,再将此球以及与它同色的5个球(共6个球)一起放回箱中。
(1)求第二次取出红球的概率;
(2)求第三次取出白球的概率;
(3)设取出白球得5分,取出红球得8分,求连续取球3次得分的期望值。
查看习题详情和答案>>已知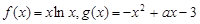
(1)求函数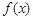 在
在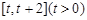 上的最小值
上的最小值
(2)对一切的 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(3)证明对一切 ,都有
,都有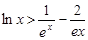 成立
成立
【解析】第一问中利用
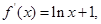 当
当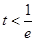 时,
时,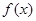 在
在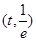 单调递减,在
单调递减,在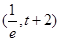 单调递增
单调递增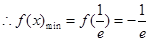 ,当
,当
 ,即
,即 时,
时,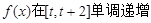 ,
,
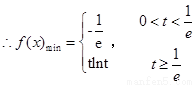
第二问中,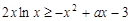 ,则
,则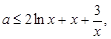 设
设 ,
,
则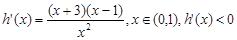 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,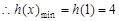 ,因为对一切
,因为对一切 ,
,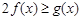 恒成立,
恒成立,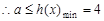
第三问中问题等价于证明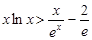 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则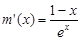 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
解:(1)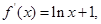 当
当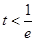 时,
时,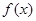 在
在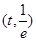 单调递减,在
单调递减,在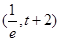 单调递增
单调递增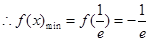 ,当
,当
 ,即
,即 时,
时,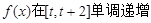 ,
,
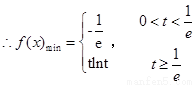 …………4分
…………4分
(2)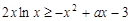 ,则
,则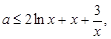 设
设 ,
,
则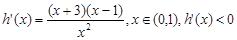 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,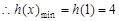 ,因为对一切
,因为对一切 ,
,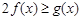 恒成立,
恒成立,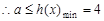 …………9分
…………9分
(3)问题等价于证明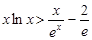 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则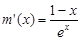 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
查看习题详情和答案>>