题目内容
已知函数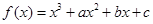 在
在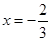 与
与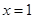 时都取得极值.
时都取得极值.
(1)求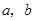 的值及函数
的值及函数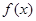 的单调区间;www.7caiedu.cn
的单调区间;www.7caiedu.cn
(2)若对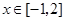 ,不等式
,不等式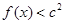 恒成立,求
恒成立,求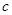 的取值范围.
的取值范围.
【解析】根据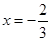 与
与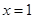 是
是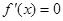 的两个根,可求出a,b的值,然后利用导数确定其单调区间即可.
的两个根,可求出a,b的值,然后利用导数确定其单调区间即可.
(2)此题本质是利用导数其函数f(x)在区间[-1,2]上的最大值,然后利用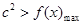 ,即可解出c的取值范围.
,即可解出c的取值范围.
【答案】
(1)f(x)=x3+ax2+bx+c,f¢(x)=3x2+2ax+b
由f¢(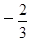 )=
)=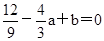 ,f¢(1)=3+2a+b=0得a=
,f¢(1)=3+2a+b=0得a=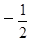 ,b=-2
,b=-2
f¢(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
|
x |
(-¥,- |
- |
(- |
1 |
(1,+¥) |
|
f¢(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
|
极大值 |
¯ |
极小值 |
|
所以函数f(x)的递增区间是(-¥,-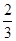 )与(1,+¥).递减区间是(-
)与(1,+¥).递减区间是(-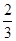 ,1)
,1)
(2)f(x)=x3-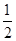 x2-2x+c,xÎ〔-1,2〕,当x=-
x2-2x+c,xÎ〔-1,2〕,当x=-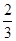 时,f(x)=
时,f(x)=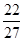 +c
+c
为极大值,而f(2)=2+c,则f(2)=2+c为最大值.
要使f(x)<c2(xÎ〔-1,2〕)恒成立,只需c2>f(2)=2+c 解得c<-1或c>2.

练习册系列答案
相关题目
 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 在
在 与
与 时都取得极值
时都取得极值 的值 (2)若对
的值 (2)若对 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围
的取值范围  在
在 与
与 时都取得极值。
时都取得极值。 的值及函数
的值及函数 的单调区间;
的单调区间; 恒成立,求
恒成立,求 的取值范围。
的取值范围。 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 在
在 与
与 时都取得极值.
时都取得极值. 的值及函数
的值及函数 的单调区间;
的单调区间; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.