网址:http://m.1010jiajiao.com/timu_id_2715[举报]
一、选择题:
1、D,2、C,3、B,4、D,5、C,6、B,7、A,8、C,9、D,10、D
二、填空题:
11、1.2; 12、 (2,+∞) ; 13、2.5 ; 14、①③④
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15、 ……(6分)
点在曲线上, ……(8分)
所求的切线方程为:,即 。 ……(12分)
16、解:(1)当时,
∴时,的最小值为1;(3分)
时,的最大值为37.(6分)
(2)函数图象的对称轴为,(8分)
∵在区间上是单调函数,∴或(10分)
故的取值范围是或.(12分)
17、解: (1)设,(1分)由得,故.(3分)
∵,∴.(
即,(5分)所以,∴. ……………7分
(2)由题意得在[-1,1]上恒成立.(9分)即在[-1,1]上恒成立.(10分)
设,其图象的对称轴为直线,所以 在[-1,1]上递减.
故只需(12分),即,解得. ……………14分
18、
解:(1)可能取的值为0、1、2、4。 ……(2分)
且,,, ……(6分)
所求的分布列为:
0
1
2
4
……(8分)
(2)由(1)可知, ……(11分)
……(14分)
19、(1)设任意实数,则
== ……………4分
.
又,∴,所以是增函数. ……………7分
法二、导数法
(2)当时,,(9分)∴, ∴,(12分)
y=g(x)= log2(x+1). ………………………14分
20、解:(1) 设x > 0,则-x < 0,∴ f (-x) = 2a(-x) + = -2ax + .2分
而 f (x) 是奇函数,
∴ f (x) = -f (-x) = 2ax- (x > 0). 4分
(2) 由(1),x > 0时,f (x) = 2ax- ,∴ f /(x) = 2a + .6分
由 f./ (x) ≥ 0得a ≥ -.
而当0 < x ≤ 1时,(- )max = -1.∴ a > -1. 8分
(3) 由 f ¢ (x) = 2a + 知,
当a ≥ 0时,在 (0, + ¥) 上,f ¢ (x) 恒大于0,故 f (x) 无最大值; 10分
当a < 0时,令f ¢ (x) = 0 得 x = .
易得 f (x) 在 (0, + ¥) 的增减性如下表所示:
x
(0,)
(, + ¥)
f ¢ (x)
+
0
-
f (x)
递增
极大
递减
12分
令 f ( ) = 2a?-= -9,即 3 = 9,得a = ±3,
当a = -3时,x = >0,
∴ a = -3时,在 (0, + ¥) 上有 f (x) max = f ( ) = -9.14分
(Ⅰ)求X所取各值的概率;
(Ⅱ)求X的分布列,并求出X的数学期望值.
(本小题满分7分)
有三张形状、大小、质地完全一致的卡片,在每张卡片上分别写上0,1,2,现从中任意抽取一张,将其上的数字记作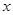 ,然后放回,再抽取一张,将其上的数字记作
,然后放回,再抽取一张,将其上的数字记作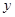 ,令
,令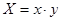 。
。
(Ⅰ)求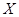 所取各值的概率;
所取各值的概率;
(Ⅱ)求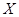 的分布列,并求出
的分布列,并求出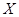 的数学期望值。
的数学期望值。
查看习题详情和答案>>
有三张形状、大小、质地完全一致的卡片,在每张卡片上分别写上0,1,2,现从中任意抽取一张,将其上的数字记作x,然后放回,再抽取一张,将其上的数字记作y,令![]() .
.
(1)求X所取各值的概率;
(2)求随机变量X的均值与方差.
查看习题详情和答案>>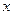 ,然后放回,再抽取一张,将其上的数字记作
,然后放回,再抽取一张,将其上的数字记作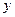 ,令
,令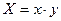 。
。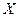 所取各值的概率;
所取各值的概率;