题目内容
有三张形状、大小、质地完全一致的卡片,在每张卡片上分别写上0,1,2,现从中任意抽取一张,将其上的数字记作x,然后放回,再抽取一张,将其上的数字记作y,令X=x•y.
(Ⅰ)求X所取各值的概率;
(Ⅱ)求X的分布列,并求出X的数学期望值.
(Ⅰ)求X所取各值的概率;
(Ⅱ)求X的分布列,并求出X的数学期望值.
分析:(Ⅰ)根据古典概型概率计算公式求解:P(A)=
;如当X=0时,表示x=0或y=0,其方法有:(0,0),(0,1),(0,2),(1,0),(2,0)共5种,而所有基本事件数是3×3种,利用
古典概型概率计算公式进行计算即可;
(Ⅱ)由题意可知随机变量X的可能取值为0,1,2,4.根据(I)中计算公式求得X取各值时的概率即可写出分布列,利用期望公式即可求得期望值.
| n(A) |
| n(Ω) |
古典概型概率计算公式进行计算即可;
(Ⅱ)由题意可知随机变量X的可能取值为0,1,2,4.根据(I)中计算公式求得X取各值时的概率即可写出分布列,利用期望公式即可求得期望值.
解答:解:(Ⅰ)P(X=0)=
=
;P(X=1)=
=
;P(X=2)=
=
;P(X=4)=
=
.…(4分)
(Ⅱ)X的分布列为
所以X的数学期望为E(X)=0×
+1×
+2×
+4×
=1.…(7分)
| 5 |
| 3×3 |
| 5 |
| 9 |
| 1×1 |
| 3×3 |
| 1 |
| 9 |
| 1+1 |
| 3×3 |
| 2 |
| 9 |
| 1 |
| 3×3 |
| 1 |
| 9 |
(Ⅱ)X的分布列为
| X | 0 | 1 | 2 | 4 | ||||||||
| P |
|
|
|
|
| 5 |
| 9 |
| 1 |
| 9 |
| 2 |
| 9 |
| 1 |
| 9 |
点评:熟练掌握古典概型的意义及概率计算公式、随机变量的分布列和数学期望是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
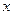 ,然后放回,再抽取一张,将其上的数字记作
,然后放回,再抽取一张,将其上的数字记作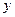 ,令
,令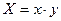 。
。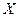 所取各值的概率;
所取各值的概率;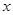 ,然后放回,再抽取一张,将其上的数字记作
,然后放回,再抽取一张,将其上的数字记作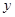 ,令
,令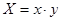 。
。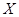 所取各值的概率;
所取各值的概率;