网址:http://m.1010jiajiao.com/timu_id_270423[举报]
一、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
C
B
C
A
B
B
A
C
二、填空题(每小题4分,共24分)
11. ; 12.
; 12. ; 13.
; 13. ; 14.
; 14. ; 15.
; 15. ; 16.(4);
; 16.(4);

19.解:∵ ,
, ,∴
,∴ ………………2分
………………2分
∴ ,
, ,………………8分
,………………8分
∴sinb=sin[(a+b)-a]=sin(a+b)cosa-cos(a+b)sina= ………………12分
………………12分
20.(1)f(x) 


 …………4分
…………4分
 ,
,
由 得,对称轴方程为:
得,对称轴方程为: ………………6分
………………6分
(2)由 得,f(x)的单调递减区间为:
得,f(x)的单调递减区间为: ,k∈Z
,k∈Z
………………9分
(3)由 ,得
,得 ,则
,则 ,
,
所以函数f(x)在区间 上的值域为
上的值域为 ………………13分
………………13分
21.解:(1)依题意,得 ,∴
,∴ ,∴
,∴ ,…………2分
,…………2分
∵最大值为2,最小值为-2,∴A=2∴ ,………………4分
,………………4分
∵图象经过(0,1),∴2sinj=1,即 又
又 ∴
∴ ,………………6分
,………………6分
∴ ………………7分
………………7分
(2)∵ ,∴-2≤ f(x) ≤ 2
,∴-2≤ f(x) ≤ 2
∴ 或
或 解得,
解得, 或
或 ………………12分
………………12分
22.解:(1)
 =2cos2x+cosx-1………………5分
=2cos2x+cosx-1………………5分
(2)要使图象至少有一公共点,须使f(x)=g(x)在上至少有一解,
令t=cos x,∵x∈(0,p) ∴x与t一一对应,且t∈(-1,1),
即方程2t2+t-1 = t2+(a+1)t + (a-3)在(-1,1)上至少有一解,………………7分
整理得:t2-at+(2-a)=0
1°一解:f(1)?f(-1)=(3 ………………9分
………………9分
2°两解(含重根的情形):
 ,解得:
,解得: ,∴
,∴ ……11分
……11分
综上所述: ………………12分
………………12分
本资料由《七彩教育网》www.7caiedu.cn 提供!
①存在实数a,使sinacosa=1;
②y=cosx的单调递增区间是[2kπ,(2k+1)π],(k∈Z);
③y=sin(
| 5π |
| 2 |
④若α,β是第一象限角,且α>β,则tanα>tanβ.
⑤函数f(x)=4sin(2x+
| π |
| 3 |
| π |
| 6 |
⑥函数y=sinx的图象的对称轴方程为x=kπ+
| π |
| 2 |
其中正确命题的序号是
①存在实数a,使sinacosa=1;
②y=cosx的单调递增区间是[2kπ,(2k+1)π],(k∈Z);
③y=sin(
 -2x)是偶函数;
-2x)是偶函数;④若α,β是第一象限角,且α>β,则tanα>tanβ.
⑤函数f(x)=4sin(2x+
 )的表达式可以改写成f(x)=4cos(2x-
)的表达式可以改写成f(x)=4cos(2x- )
)⑥函数y=sinx的图象的对称轴方程为
 .
.其中正确命题的序号是 .(注:把你认为正确命题的序号都填上) 查看习题详情和答案>>
给出下列说法:
①正切函数在定义域内是增函数;
②函数f(x)=2tan  的单调递增区间是
的单调递增区间是 (k∈Z);
(k∈Z);
③函数y=2tan 的定义域是
的定义域是 ;
;
④函数y=tan x+1在 上的最大值为
上的最大值为 +1,最小值为0.
+1,最小值为0.
其中正确说法的序号是________.
查看习题详情和答案>>
 的单调递增区间是
的单调递增区间是 (k∈Z);
(k∈Z);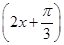 的定义域是
的定义域是 ;
; 上的最大值为
上的最大值为 +1,最小值为0.
+1,最小值为0. 的单调递增区间是
的单调递增区间是 (k∈Z);
(k∈Z); 的定义域是
的定义域是 ;
; 上的最大值为
上的最大值为 +1,最小值为0.
+1,最小值为0.