网址:http://m.1010jiajiao.com/timu_id_267151[举报]
1.解析: ,故选A。
,故选A。
2.解析:∵
 ,
,
故选B。
3.解析:由 ,得
,得 ,此时
,此时 ,所以,
,所以, ,故选C。
,故选C。
4.解析:显然,若 与
与 共线,则
共线,则 与
与 共线;若
共线;若 与
与 共线,则
共线,则 ,即
,即
 ,得
,得 ,∴
,∴ 与
与 共线,∴
共线,∴ 与
与 共线是
共线是 与
与 共线的充要条件,故选C。
共线的充要条件,故选C。
5.解析:设公差为 ,由题意得,
,由题意得, ;
; ,解得
,解得 或
或 ,故选C。
,故选C。
6.解析:∵双曲线 的右焦点到一条渐近线的距离等于焦距的
的右焦点到一条渐近线的距离等于焦距的 ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴
,∴ ,∴双曲线的离心率是
,∴双曲线的离心率是 。故选B.
。故选B.
7.解析:∵ 、
、 为正实数,∴
为正实数,∴ ,∴
,∴ ;由均值不等式得
;由均值不等式得 恒成立,
恒成立, ,故②不恒成立,又因为函数
,故②不恒成立,又因为函数 在
在 是增函数,∴
是增函数,∴ ,故恒成立的不等式是①③④。故选C.
,故恒成立的不等式是①③④。故选C.
8.解析:∵ ,∴
,∴ 在区间
在区间 上恒成立,即
上恒成立,即 在区间
在区间 上恒成立,∴
上恒成立,∴ ,故选D。
,故选D。
9.解析:∵

 ,此函数的最小值为
,此函数的最小值为 ,故选C。
,故选C。
10.解析:如图,∵正三角形 的边长为
的边长为 ,∴
,∴ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,故选D。
,故选D。
11.解析:∵ 在区间
在区间 上是增函数且
上是增函数且 ,∴其反函数
,∴其反函数 在区间上
在区间上 是增函数,∴
是增函数,∴

 ,故选A
,故选A
12.解析:如图,①当 或
或 时,圆面
时,圆面 被分成2块,涂色方法有20种;②当
被分成2块,涂色方法有20种;②当 或
或 时,圆面
时,圆面 被分成3块,涂色方法有60种;
被分成3块,涂色方法有60种;
③当 时,圆面
时,圆面 被分成4块,涂色方法有120种,所以m的取值范围是
被分成4块,涂色方法有120种,所以m的取值范围是 ,故选A。
,故选A。
13.解析:做出 表示的平面区域如图,当直线
表示的平面区域如图,当直线 经过点
经过点 时,
时, 取得最大值5。
取得最大值5。
 14.解析:∵
14.解析:∵ ,∴
,∴ 时,
时, ,又
,又 时,
时, 满足上式,因此,
满足上式,因此, ,
,
∴ 。
。
 15.解析:设正四面体的棱长为
15.解析:设正四面体的棱长为 ,连
,连 ,取
,取 的中点
的中点 ,连
,连 ,∵
,∵ 为
为 的中点,∴
的中点,∴ ∥
∥ ,∴
,∴ 或其补角为
或其补角为 与
与 所成角,∵
所成角,∵ ,
, ,∴
,∴ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴
,∴ 与
与 所成角的余弦值为
所成角的余弦值为 。
。
 16.解析:∵
16.解析:∵ ,∴
,∴ ,∵点
,∵点 为
为 的准线与
的准线与 轴的交点,由向量的加法法则及抛物线的对称性可知,点
轴的交点,由向量的加法法则及抛物线的对称性可知,点 为抛物线上关于轴对称的两点且做出图形如右图,其中
为抛物线上关于轴对称的两点且做出图形如右图,其中 为点
为点 到准线的距离,四边形
到准线的距离,四边形 为菱形,∴
为菱形,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴向量
,∴向量 与
与 的夹角为
的夹角为 。
。
17.(10分)解析:(Ⅰ)由正弦定理得, ,
, ,…2分
,…2分
∴ ,
, ,………4分
,………4分
(Ⅱ)∵ ,
, ,∴
,∴ ,∴
,∴ ,………………………6分
,………………………6分
又∵ ,∴
,∴ ,∴
,∴ ,………………………8分
,………………………8分
∴ 。………………………10分
。………………………10分
18.解析:(Ⅰ)∵ ,∴
,∴ ;……………………理3文4分
;……………………理3文4分
(Ⅱ)∵三科会考不合格的概率均为 ,∴学生甲不能拿到高中毕业证的概率
,∴学生甲不能拿到高中毕业证的概率 ;……………………理6文8分
;……………………理6文8分
(Ⅲ)∵每科得A,B的概率分别为 ,∴学生甲被评为三好学生的概率为
,∴学生甲被评为三好学生的概率为 。……………………12分
。……………………12分
(理)∵
 ,
, ,
, ,
, 。……………………9分
。……………………9分
∴ 的分布列如下表:
的分布列如下表:

0
1
2
3





∴ 的数学期望
的数学期望
 。……………………12分
。……………………12分
19.(12分)解析:(Ⅰ) 时,
时,
 ,
,
 ,
,


由 得,
得, 或
或 ………3分
………3分







+
0
-
0
+

递增
极大值
递减
极小值
递增
 ,
, ………………………6分
………………………6分
(Ⅱ) 在定义域
在定义域 上是增函数,
上是增函数,

 对
对 恒成立,即
恒成立,即
 ………………………9分
………………………9分
又 (当且仅当
(当且仅当 时,
时, )
)

 ………………………4分
………………………4分

20.解析:(Ⅰ)∵ ∥
∥ ,
, ,∴
,∴ ,∵
,∵ 底面
底面 ,∴
,∴ ,∴
,∴ 平面
平面 ,∴
,∴ ,又∵
,又∵ 平面
平面 ,∴
,∴ ,∴
,∴ 平面
平面 ,∴
,∴ 。………………………4分
。………………………4分
(Ⅱ)∵ 平面
平面 ,∴
,∴ ,
, ,∴
,∴ 为二面角
为二面角 的平面角,………………………6分
的平面角,………………………6分
 ,
, ,∴
,∴ ,又∵
,又∵ 平面
平面 ,
, ,∴
,∴ ,∴二面角
,∴二面角 的正切值的大小为
的正切值的大小为 。………………………8分
。………………………8分
(Ⅲ)过点 做
做 ∥
∥ ,交
,交 于点
于点 ,∵
,∵ 平面
平面 ,∴
,∴ 为
为 在平面
在平面 内的射影,∴
内的射影,∴ 为
为 与平面
与平面 所成的角,………………………10分
所成的角,………………………10分
 ∵
∵ ,∴
,∴ ,又∵
,又∵ ∥
∥ ,∴
,∴ 和
和 与平面
与平面 所成的角相等,∴
所成的角相等,∴ 与平面
与平面 所成角的正切值为
所成角的正切值为 。………………………12分
。………………………12分
解法2:如图建立空间直角坐标系,(Ⅰ)∵, ,∴点
,∴点 的坐标分别是
的坐标分别是 ,
, ,
,
 ,∴
,∴ ,
, ,设
,设 ,∵
,∵ 平面
平面 ,∴
,∴ ,∴
,∴ ,取
,取 ,∴
,∴ ,∴
,∴ 。………………………4分
。………………………4分
(Ⅱ)设二面角 的大小为
的大小为 ,∵平面
,∵平面 的法向量是
的法向量是 ,平面
,平面 的法向量是
的法向量是 ,∴
,∴ ,∴
,∴ ,∴二面角
,∴二面角 的正切值的大小为
的正切值的大小为 。………………………8分
。………………………8分
(Ⅲ)设 与平面
与平面 所成角的大小为
所成角的大小为 ,∵平面
,∵平面 的法向量是
的法向量是 ,
, ,∴
,∴ ,∴
,∴ ,∴
,∴ 与平面
与平面 所成角的正切值为
所成角的正切值为 。………………………12分
。………………………12分
21.(Ⅰ) 解析:如图,设右准线 与
与 轴的交点为
轴的交点为 ,过点
,过点 分别向
分别向 轴及右准线引垂线
轴及右准线引垂线 ,∵
,∵ ,∴
,∴ ,又∵
,又∵ ∥
∥ ,∴
,∴
 ,………………………2分
,………………………2分
∴ ,又∵
,又∵ ,∴
,∴ ,又∵
,又∵ ,解得
,解得 ,∴
,∴ ,∴双曲线
,∴双曲线 的方程为
的方程为 。………………………4分
。………………………4分
(Ⅱ)联立方程组  消
消 得:
得:
由直线 与双曲线
与双曲线 交于不同的两点得:
交于不同的两点得:
即  于是
于是  ,且
,且 ………………①………………………6分
………………①………………………6分
设 、
、 ,则
,则

 ……………………9分
……………………9分
又 ,所以
,所以 ,解得
,解得
 ……………②
……………②
由①和②得
 即
即 或
或
故 的取值范围为
的取值范围为 。………………………12分
。………………………12分
22.(12分)解析:(Ⅰ)∵ ,∴
,∴ ,∴
,∴ ,∴数列
,∴数列 是等差数列,………………………2分
是等差数列,………………………2分
又∵ ,
, ,∴公差为2,
,∴公差为2,
∴ ,………………………4分
,………………………4分
(Ⅱ)∵ ,∴
,∴ ,
,
∴数列 是公比为2的等比数列,
是公比为2的等比数列,
∵ ,∴
,∴ ,………………………6分
,………………………6分
(Ⅲ)∵ ,
,
∴ ………………………8分
………………………8分
∴ ………………………10分
………………………10分
 ∵
∵ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ………………………12分
………………………12分
已知中心在坐标原点,焦点在 轴上的椭圆C;其长轴长等于4,离心率为
轴上的椭圆C;其长轴长等于4,离心率为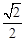 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点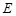 (0,1), 问是否存在直线
(0,1), 问是否存在直线 与椭圆
与椭圆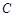 交于
交于 两点,且
两点,且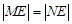 ?若存在,求出
?若存在,求出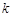 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【解析】本试题主要考查了椭圆的方程的求解,直线与椭圆的位置关系的运用。
第一问中,可设椭圆的标准方程为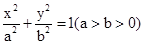
则由长轴长等于4,即2a=4,所以a=2.又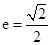 ,所以
,所以 ,
,
又由于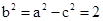
所求椭圆C的标准方程为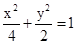
第二问中,
假设存在这样的直线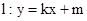 ,设
,设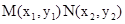 ,MN的中点为
,MN的中点为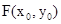
因为|ME|=|NE|所以MN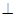 EF所以
EF所以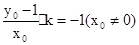
(i)其中若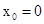 时,则K=0,显然直线
时,则K=0,显然直线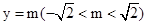 符合题意;
符合题意;
(ii)下面仅考虑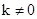 情形:
情形:
由 ,得,
,得,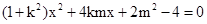
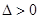 ,得
,得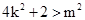
代入1,2式中得到范围。
(Ⅰ) 可设椭圆的标准方程为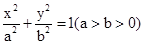
则由长轴长等于4,即2a=4,所以a=2.又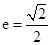 ,所以
,所以 ,
,
又由于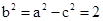
所求椭圆C的标准方程为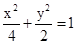
(Ⅱ) 假设存在这样的直线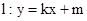 ,设
,设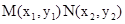 ,MN的中点为
,MN的中点为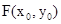
因为|ME|=|NE|所以MN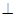 EF所以
EF所以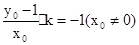
(i)其中若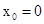 时,则K=0,显然直线
时,则K=0,显然直线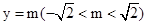 符合题意;
符合题意;
(ii)下面仅考虑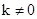 情形:
情形:
由 ,得,
,得,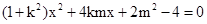
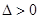 ,得
,得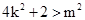 ……② ……………………9分
……② ……………………9分
则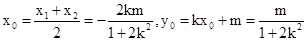 .
.
代入①式得,解得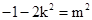 ………………………………………12分
………………………………………12分
代入②式得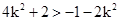 ,得
,得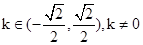 .
.
综上(i)(ii)可知,存在这样的直线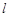 ,其斜率k的取值范围是
,其斜率k的取值范围是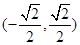
查看习题详情和答案>>
 的直线l,交双曲线左支于A,B两点,交y轴于点C,且满足|PA|· |PB|=|PC|2。
的直线l,交双曲线左支于A,B两点,交y轴于点C,且满足|PA|· |PB|=|PC|2。(1)求双曲线的标准方程;
(2)设点M为双曲线上一动点,点N为圆x2+(y-2)2=
 上一动点,求|MN|的取值范围。
上一动点,求|MN|的取值范围。 sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π。
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π。 ,求f(θ)的值。
,求f(θ)的值。 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值。
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值。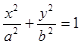
 >
> >
> 与直线
与直线 交于
交于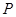 、
、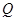 两点,且
两点,且 ,其
,其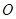 为坐标原点。
为坐标原点。 的值;
的值; 满足
满足 ,求椭圆长轴的取值范围。
,求椭圆长轴的取值范围。