摘要：过点C作CN⊥AH于N.交BD于K. 在Rt△BCK中.∠CBK=90°-60°=30°
网址：http://m.1010jiajiao.com/timu_id_261[举报]
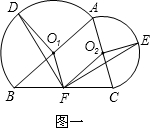
如图一，在△ABC中，分别以AB，AC为直径在△ABC外作半圆O1和半圆O2，其中O1和O2分别为两个半圆的圆心．F是边BC的中点，点D和点E分别为两个半圆圆弧的中点．
（1）连接O1F，O1D，DF，O2F，O2E，EF，证明：△DO1F≌△FO2E；
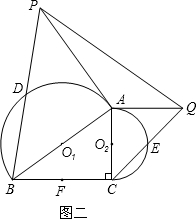
（2）如图二，过点A分别作半圆O1和半圆O2的切线，交BD的延长线和CE的延长线于点P和点Q，连接PQ，若∠ACB=90°，DB=5，CE=3，求线段PQ的长；
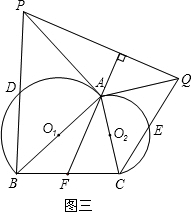
（3）如图三，过点A作半圆O2的切线，交CE的延长线于点Q，过点Q作直线FA的垂线，交BD的延长线于点P，连接PA．证明：PA是半圆O1的切线．
查看习题详情和答案>>
（1）连接O1F，O1D，DF，O2F，O2E，EF，证明：△DO1F≌△FO2E；
（2）如图二，过点A分别作半圆O1和半圆O2的切线，交BD的延长线和CE的延长线于点P和点Q，连接PQ，若∠ACB=90°，DB=5，CE=3，求线段PQ的长；
（3）如图三，过点A作半圆O2的切线，交CE的延长线于点Q，过点Q作直线FA的垂线，交BD的延长线于点P，连接PA．证明：PA是半圆O1的切线．
查看习题详情和答案>>
观察本题的三个图形，思考下列问题
（1）如图1，正方形ABCD中，点M是CD上异于端点的任意一点，过点C作CN⊥BM于O，且交AD于N点．求证：BM=CN；
（2）如图2，等边△ABC中，点M是CA上异于端点的任意一点，过点C作射线CN交AB于点N、交BM于点O，且使∠BOC=120°．
请你判断此时BM与CN的大小关系，并证明你的结论．
（3）如图3，正n边形ABCDE…An中，点M是CD上异于端点的任意一点，过点C作射线CN交DE于点N、交BM于点O，且使BM=CN．设此时∠BOC的大小为y，请你写出y与n之间的函数关系式．
查看习题详情和答案>>
（1）如图1，正方形ABCD中，点M是CD上异于端点的任意一点，过点C作CN⊥BM于O，且交AD于N点．求证：BM=CN；
（2）如图2，等边△ABC中，点M是CA上异于端点的任意一点，过点C作射线CN交AB于点N、交BM于点O，且使∠BOC=120°．
请你判断此时BM与CN的大小关系，并证明你的结论．
（3）如图3，正n边形ABCDE…An中，点M是CD上异于端点的任意一点，过点C作射线CN交DE于点N、交BM于点O，且使BM=CN．设此时∠BOC的大小为y，请你写出y与n之间的函数关系式．
查看习题详情和答案>>
已知：如图，四边形ABCD是等腰梯形，其中AD∥BC，AD=2，BC=4，AB=DC=2，点M从点B开始，以每秒1个单位的速度向点C运动；点N从点D开始，沿D→A→B方向，以每秒1个单位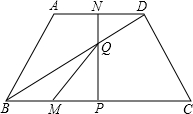
的速度向点B运动．若点M、N同时开始运动，其中一点到达终点，另一点也停止运动，运动时间为t（t＞0）．过点N作NP⊥BC与P，交BD于点Q．
（1）点D到BC的距离为 ；
（2）求出t为何值时，QM∥AB；
（3）设△BMQ的面积为S，求S与t的函数关系式；
（4）求出t为何值时，△BMQ为直角三角形． 查看习题详情和答案>>
的速度向点B运动．若点M、N同时开始运动，其中一点到达终点，另一点也停止运动，运动时间为t（t＞0）．过点N作NP⊥BC与P，交BD于点Q．（1）点D到BC的距离为
（2）求出t为何值时，QM∥AB；
（3）设△BMQ的面积为S，求S与t的函数关系式；
（4）求出t为何值时，△BMQ为直角三角形． 查看习题详情和答案>>
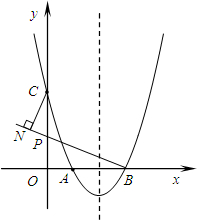（2013•天桥区二模）如图，抛物线y=ax2+bx+3过点A（1，0），B（3，0），与y轴相交于点C．
和半圆
，其中
，证明：
；
