题目内容
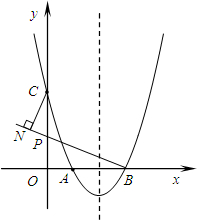 (2013•天桥区二模)如图,抛物线y=ax2+bx+3过点A(1,0),B(3,0),与y轴相交于点C.
(2013•天桥区二模)如图,抛物线y=ax2+bx+3过点A(1,0),B(3,0),与y轴相交于点C.(1)求抛物线的解析式;
(2)若点E为抛物线对称轴上的一点,请探索抛物线上是否存在点F,使以A,B,E,F为顶点的四边形为平行四边形?若存在,请求出所有点F的坐标;若不存在,请说明理由;
(3)若点P为线段OC上的动点,连接BP,过点C作CN垂直于直线BP,垂足为N,当点P从点O运动到点C时,求点N运动路径的长.
分析:(1)将点A、B的坐标代入抛物线解析式,可得出a、b的值,继而得出抛物线的解析式;
(2)分两种情况讨论,①E、F在AB同侧,此时EF为平行四边形的边,②E、F在AB异侧,此时EF为平行四边形的对角线,根据平行线的性质即可得出点F的坐标;
(3)连接BC,可得点N的路径是以BC的中点M为圆心,BC长的一半为半径的
,求出
的长度即可.
(2)分两种情况讨论,①E、F在AB同侧,此时EF为平行四边形的边,②E、F在AB异侧,此时EF为平行四边形的对角线,根据平行线的性质即可得出点F的坐标;
(3)连接BC,可得点N的路径是以BC的中点M为圆心,BC长的一半为半径的
 |
| OC |
 |
| OC |
解答: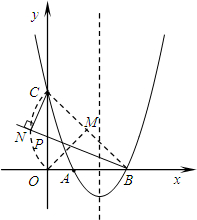 解:(1)将A(1,0)(3,0)代入y=ax2+bx+3得:
解:(1)将A(1,0)(3,0)代入y=ax2+bx+3得:
,
解得:
,
∴y=x2-4x+3.
(2)①设F(x,x2-4x+3),若E,F在AB的同侧,则EF=AB=2,
∵点E在抛物线的对称轴上,
∴|x-2|=2,
∴x=0或x=4,
∴F1(0,3),F2(4,3).
②若E,F在AB异侧,则F与抛物线的顶点重合,即F3(2,-1),
∴存在点F1(0,3),F2(4,3),F3(2,-1),使以A,B,E,F为顶点的四边形为平行四边形.
(3)连接BC,
∵∠BNC=90°,
∴点N的路径是以BC的中点M为圆心,BC长的一半为半径的
,
连接OM,
∵OB=OC=3,
∴OM⊥BC,
∴∠OMC=90°,
∵BC=
=3
,
∴OM=
∴l
=
•
=
π.
 解:(1)将A(1,0)(3,0)代入y=ax2+bx+3得:
解:(1)将A(1,0)(3,0)代入y=ax2+bx+3得:
|
解得:
|
∴y=x2-4x+3.
(2)①设F(x,x2-4x+3),若E,F在AB的同侧,则EF=AB=2,
∵点E在抛物线的对称轴上,
∴|x-2|=2,
∴x=0或x=4,
∴F1(0,3),F2(4,3).
②若E,F在AB异侧,则F与抛物线的顶点重合,即F3(2,-1),
∴存在点F1(0,3),F2(4,3),F3(2,-1),使以A,B,E,F为顶点的四边形为平行四边形.
(3)连接BC,
∵∠BNC=90°,
∴点N的路径是以BC的中点M为圆心,BC长的一半为半径的
 |
| OC |
连接OM,
∵OB=OC=3,
∴OM⊥BC,
∴∠OMC=90°,
∵BC=
| OB2+OC2 |
| 2 |
∴OM=
3
| ||
| 2 |
∴l
 |
| oc |
| 90π |
| 180 |
3
| ||
| 2 |
3
| ||
| 4 |
点评:本题考查了二次函数的综合题,涉及了待定系数法求二次函数解析式、平行四边形的性质及点的运动轨迹,难点在第三问,连接BC,根据∠BNC=90°,判断出点N的运动路径是解题的关键,此类题目常以压轴题出现,同学们要注意培养自己解答综合题的能力.

练习册系列答案
相关题目
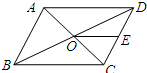 (2013•天桥区二模)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是( )
(2013•天桥区二模)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是( )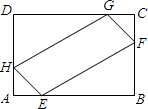 (2013•天桥区二模)在矩形ABCD的各边AB,BC,CD和DA上分别选取点E,F,G,H,使得AE=AH=CF=CG,如果AB=60,BC=40,四边形EFGH的最大面积是( )
(2013•天桥区二模)在矩形ABCD的各边AB,BC,CD和DA上分别选取点E,F,G,H,使得AE=AH=CF=CG,如果AB=60,BC=40,四边形EFGH的最大面积是( )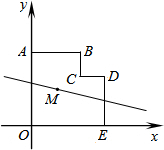 (2013•天桥区二模)如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则下列各点在直线l上的是( )
(2013•天桥区二模)如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则下列各点在直线l上的是( )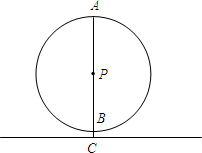 (2013•天桥区二模)如图所示,⊙P表示的是一个摩天轮,最高处A到地面的距离是80.5米,最低处B到地面的距离是0.5米.小红由B处登上摩天轮,乘坐一周需要12分钟.乘坐一周的过程中,小红距离地面的高度是60.5米的时刻是第
(2013•天桥区二模)如图所示,⊙P表示的是一个摩天轮,最高处A到地面的距离是80.5米,最低处B到地面的距离是0.5米.小红由B处登上摩天轮,乘坐一周需要12分钟.乘坐一周的过程中,小红距离地面的高度是60.5米的时刻是第