摘要:由 得 且 ----13分
网址:http://m.1010jiajiao.com/timu_id_25776[举报]
(13分)已知椭圆![]() 的长轴长为4,A,B,C是椭圆上的三点,点A是长轴的一个顶点,BC过椭圆的中心O,且
的长轴长为4,A,B,C是椭圆上的三点,点A是长轴的一个顶点,BC过椭圆的中心O,且![]() ,
,![]() ,如图.
,如图.
(Ⅰ)求椭圆的方程;
(Ⅱ)如果椭圆上的两点P,Q使![]() 的平分线垂直于OA,是否总存在实数
的平分线垂直于OA,是否总存在实数![]() ,使得
,使得![]() ?请说明理由.
?请说明理由.

(13分)已知椭圆C的中心在坐标原点,离心率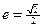 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线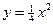 的焦点重合.
的焦点重合.
(1)求椭圆C的方程;
(2)过点S(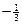 ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
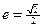 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线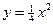 的焦点重合.
的焦点重合.(1)求椭圆C的方程;
(2)过点S(
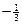 ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.(本题13分)已知数列{an}中,a1 = t (t≠0,且t≠1),a2 = t2.且当x = t时,函数f (x) =![]() (an an 1)x2 (an + 1 an) x (n≥2)取得极值.
(an an 1)x2 (an + 1 an) x (n≥2)取得极值.
(1)求证:数列{an + 1 an}是等比数列;
(2)若bn = an ln |an| (n∈N+),求数列{bn}的前n项的和Sn;
(3)当t = ![]() 时,数列{bn}中是否存在最大项?如果存在,说明是第几项,如果不存在,请说明理由.
时,数列{bn}中是否存在最大项?如果存在,说明是第几项,如果不存在,请说明理由.
 的左右焦点分别为
的左右焦点分别为 ,
, ,上顶点为
,上顶点为 ,过点
,过点 垂直的直线交
垂直的直线交 轴负半轴于
轴负半轴于 点,且
点,且 是
是 的中点.
的中点.
 的圆恰好与直线
的圆恰好与直线 相切,求椭圆
相切,求椭圆 的方程;
的方程; 作斜率为
作斜率为 的直线
的直线 与椭圆相交于
与椭圆相交于 两点,在
两点,在 使得以
使得以 为邻边的平行四边形为菱形,如果存在,求出
为邻边的平行四边形为菱形,如果存在,求出 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线 的焦点,离心率
的焦点,离心率 ,过椭圆的右焦点
,过椭圆的右焦点 作不与坐标轴垂直的直线
作不与坐标轴垂直的直线 ,交椭圆于A、B两点.
,交椭圆于A、B两点. ,求
,求 取值范围;
取值范围;