摘要:当且仅当.即时.有最小值------8分即每隔10天购买一次饲料才能使平均每天支付的总费用最小.
网址:http://m.1010jiajiao.com/timu_id_25745[举报]
一段长为32米的篱笆围成一个一边靠墙的矩形菜园,墙长18米,问这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
【解析】解:令矩形与墙垂直的两边为宽并设矩形宽为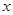 ,则长为
,则长为
所以矩形的面积 (
( ) (4分
) (4分 =128 (8分)
=128 (8分)
当且仅当 时,即
时,即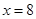 时等号成立,此时
时等号成立,此时 有最大值128
有最大值128
所以当矩形的长为 =16,宽为8时,
=16,宽为8时,
菜园面积最大,最大面积为128 (13分)答:当矩形的长为16米,宽为8米时。菜园面积最大,最大面积为128平方米(注:也可用二次函数模型解答)
查看习题详情和答案>>
对于问题:“已知两个正数x,y满足x+y=2,求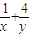 的最小值”,给出如下一种解法:
的最小值”,给出如下一种解法:
Qx+y=2,∴ =
=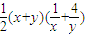 =
=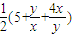 ,
,
Qx>0,y>0,∴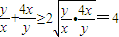 ,∴
,∴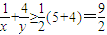 ,
,
当且仅当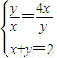 ,即
,即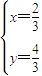 时,
时,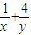 取最小值
取最小值 .
.
参考上述解法,已知A,B,C是△ABC的三个内角,则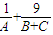 的最小值为 .
查看习题详情和答案>>
的最小值为 .
查看习题详情和答案>>
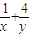 的最小值”,给出如下一种解法:
的最小值”,给出如下一种解法:Qx+y=2,∴
 =
=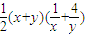 =
=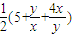 ,
,Qx>0,y>0,∴
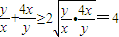 ,∴
,∴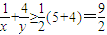 ,
,当且仅当
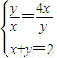 ,即
,即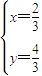 时,
时,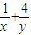 取最小值
取最小值 .
.参考上述解法,已知A,B,C是△ABC的三个内角,则
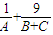 的最小值为 .
查看习题详情和答案>>
的最小值为 .
查看习题详情和答案>>
 给出下列四个命题:
给出下列四个命题: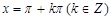 时,该函数取得最小值是-1;
时,该函数取得最小值是-1;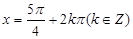 对称;
对称;