题目内容
对于问题:“已知两个正数x,y满足x+y=2,求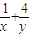 的最小值”,给出如下一种解法:
的最小值”,给出如下一种解法:Qx+y=2,∴
 =
=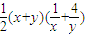 =
=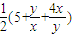 ,
,Qx>0,y>0,∴
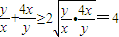 ,∴
,∴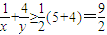 ,
,当且仅当
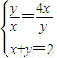 ,即
,即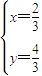 时,
时,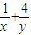 取最小值
取最小值 .
.参考上述解法,已知A,B,C是△ABC的三个内角,则
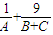 的最小值为 .
的最小值为 .
【答案】分析:参考上述解法,根据题意可知A+B+C=π设A=α,B+C=β则 α+β=π,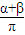 =1,将
=1,将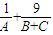 即
即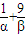 乘以1化简整理,利用基本不等式即可求出最小值,注意等号成立的条件.
乘以1化简整理,利用基本不等式即可求出最小值,注意等号成立的条件.
解答:解:A+B+C=π,即A+B+C=π,设A=α,B+C=β,则 α+β=π,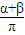 =1,
=1,
参考上述解法,则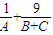 =
=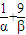 =(
=(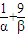 )(α+β)
)(α+β)  =
= (10+
(10+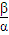 +
+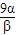 )≥
)≥ (10+6),
(10+6),
当且仅当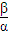 =
=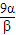 ,即3α=β时等号成立.
,即3α=β时等号成立.
故答案为: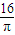 .
.
点评:本小题主要考查类比推理、基本不等式求最值,解题的关键是等号成立的条件,中档题.
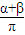 =1,将
=1,将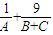 即
即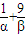 乘以1化简整理,利用基本不等式即可求出最小值,注意等号成立的条件.
乘以1化简整理,利用基本不等式即可求出最小值,注意等号成立的条件.解答:解:A+B+C=π,即A+B+C=π,设A=α,B+C=β,则 α+β=π,
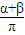 =1,
=1,参考上述解法,则
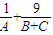 =
=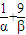 =(
=(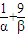 )(α+β)
)(α+β)  =
= (10+
(10+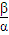 +
+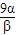 )≥
)≥ (10+6),
(10+6),当且仅当
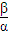 =
=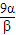 ,即3α=β时等号成立.
,即3α=β时等号成立.故答案为:
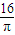 .
.点评:本小题主要考查类比推理、基本不等式求最值,解题的关键是等号成立的条件,中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目