摘要:(Ⅲ)设.存在数列使得.试求数列的前项和. 河北区2008―2009学年度高三年级总复习质量检测二数 学题号12345678910答案BACBDCDBAC
网址:http://m.1010jiajiao.com/timu_id_256665[举报]
在数列{an}和{bn}中,an=an,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.设A={a1,a2,a3,…},B={b1,b2,b3,…},试问在区间[1,a]上是否存在实数b使得C=A∩B≠∅.若存在,求出b的一切可能的取值及相应的集合C;若不存在,试说明理由.
查看习题详情和答案>>
在数列{an}和{bn}中,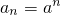 ,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.设A={a1,a2,a3,…},B={b1,b2,b3,…},试问在区间[1,a]上是否存在实数b使得C=A∩B≠∅.若存在,求出b的一切可能的取值及相应的集合C;若不存在,试说明理由.
,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.设A={a1,a2,a3,…},B={b1,b2,b3,…},试问在区间[1,a]上是否存在实数b使得C=A∩B≠∅.若存在,求出b的一切可能的取值及相应的集合C;若不存在,试说明理由.
查看习题详情和答案>>
在数列{an}和{bn}中,an=an,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.
(Ⅰ)若a1=b1,a2<b2,求数列{bn}的前n项和;
(Ⅱ)证明:当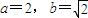 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;
(Ⅲ)设A={a1,a2,a3,…},B={b1,b2,b3,…},试问在区间[1,a]上是否存在实数b使得C=A∩B≠∅.若存在,求出b的一切可能的取值及相应的集合C;若不存在,试说明理由.
查看习题详情和答案>>
(Ⅰ)若a1=b1,a2<b2,求数列{bn}的前n项和;
(Ⅱ)证明:当
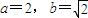 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;(Ⅲ)设A={a1,a2,a3,…},B={b1,b2,b3,…},试问在区间[1,a]上是否存在实数b使得C=A∩B≠∅.若存在,求出b的一切可能的取值及相应的集合C;若不存在,试说明理由.
查看习题详情和答案>>
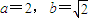 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;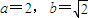 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;