摘要:1.已知函数在处的导数为.若为函数的极大值.则必有
网址:http://m.1010jiajiao.com/timu_id_24901[举报]
已知函数 在
在 处取得极值2.
处取得极值2.
⑴ 求函数 的解析式;
的解析式;
⑵ 若函数 在区间
在区间 上是单调函数,求实数m的取值范围;
上是单调函数,求实数m的取值范围;
【解析】第一问中利用导数
又f(x)在x=1处取得极值2,所以 ,
,
所以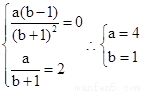
第二问中,
因为 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有 ,得
,得
解:⑴ 求导 ,又f(x)在x=1处取得极值2,所以
,又f(x)在x=1处取得极值2,所以 ,即
,即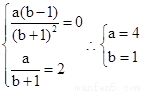 ,所以
,所以 …………6分
…………6分
⑵ 因为 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有 ,得
,得 , …………9分
, …………9分
当f(x)在区间(m,2m+1)上单调递减,则有
得 …………12分
…………12分
.综上所述,当 时,f(x)在(m,2m+1)上单调递增,当
时,f(x)在(m,2m+1)上单调递增,当 时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是
时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是 或
或
查看习题详情和答案>>
已知函数f(x)=alnx-bx2图象上一点P(2,f(2))处的切线方程为y=-3x+2ln2+2.
(Ⅰ)求a,b的值;
(Ⅱ)若方程f(x)+m=0在[
,e]内有两个不等实根,求m的取值范围(其中e为自然对数的底数);
(Ⅲ)令g(x)=f(x)-kx,若g(x)的图象与x轴交于A(x1,0),B(x2,0)(其中x1<x2),AB的中点为C(x0,0),求证:g(x)在x0处的导数g′(x0)≠0. 查看习题详情和答案>>
(Ⅰ)求a,b的值;
(Ⅱ)若方程f(x)+m=0在[
| 1 | e |
(Ⅲ)令g(x)=f(x)-kx,若g(x)的图象与x轴交于A(x1,0),B(x2,0)(其中x1<x2),AB的中点为C(x0,0),求证:g(x)在x0处的导数g′(x0)≠0. 查看习题详情和答案>>