摘要:19.(1)证明:数列是等差数列.设公差为.则对恒成立.
网址:http://m.1010jiajiao.com/timu_id_248745[举报]
设等差数列{an}的前n项和为Sn,且Sn=
nan+an-c(c是常数,n∈N*),a2=6.
(Ⅰ)求c的值及数列{an}的通项公式;
(Ⅱ)证明:
+
+…+
<
.
查看习题详情和答案>>
| 1 |
| 2 |
(Ⅰ)求c的值及数列{an}的通项公式;
(Ⅱ)证明:
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| 1 |
| 8 |
已知{an}是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合A={(an,
)|n∈N*},B={(x,y)|
x2-y2=1,x,y∈R}.试问下列结论是否正确,如果正确,请给予证明;如果不正确,请举例说明:
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2)A∩B至多有一个元素;
(3)当a1≠0时,一定有A∩B≠∅. 查看习题详情和答案>>
| Sn |
| n |
| 1 |
| 4 |
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2)A∩B至多有一个元素;
(3)当a1≠0时,一定有A∩B≠∅. 查看习题详情和答案>>
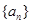 的公差为
的公差为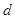 ,点
,点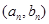 在函数
在函数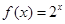 的图象上(
的图象上(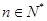 ).
).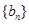 是等比数列;
是等比数列;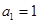 ,学科网函数
,学科网函数 的图象在点
的图象在点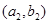 处的切线在
处的切线在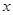 轴上的截距为
轴上的截距为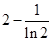 ,求数列
,求数列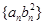 的前
的前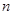 项和
项和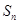 .
.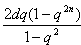 ,n∈N*。
,n∈N*。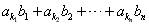 ,c2=
,c2=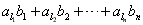 ,证明c1≠c2。
,证明c1≠c2。