网址:http://m.1010jiajiao.com/timu_id_246299[举报]
一、 选择题: ACAAD;CBDBC
二、 填空题:
三、解答题:
16.解:
17.解:
(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)…………………….4分
(2)点M不在x轴上的坐标共有12种:
(-2,-2),(-2,0),(-2,1),(-2,3);(1,-2),(1,0),(1,1),(1,3);
(3,-2),(3,0),(3,1),(3,3)
所以点M不在x轴上的概率是.files/image174.gif) ………………………………………..8分
………………………………………..8分
(3)点M正好落在区域.files/image129.gif) 上的坐标共有3种:(1,1),(1,3),(3,1)
上的坐标共有3种:(1,1),(1,3),(3,1)
故M正好落在该区域上的概率为.files/image176.gif) …………………………………………………12分
…………………………………………………12分
18、解:
(1)判断:AB//平面DEF………………………………………………..2分
AC,BC的中点,有
EF//AB………………..5分
又因
所以
AB//平面DEF……………..7分
故EM.files/image133.gif) 平面BCD 于是EM是三棱锥E-CDF的高……………………………..9分
平面BCD 于是EM是三棱锥E-CDF的高……………………………..9分
EM=.files/image192.gif) ……………………………………………………………………11分
……………………………………………………………………11分
故三棱锥C-DEF的体积为
19、解:
所以所求的椭圆的方程是:.files/image204.gif) ………………………………………….6分
………………………………………….6分
.files/image210.gif) 在C内,故过
在C内,故过.files/image210.gif) 没有圆C的切线……………………………………………….8分
没有圆C的切线……………………………………………….8分
20、解:
2
(2)1
2
21.解:
当n为偶数时,
当n为奇数时,
当n为奇数时,
当n为偶数时,
本资料由《七彩教育网》www.7caiedu.cn 提供!
(本小题满分14分)已知椭圆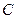 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在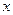 轴上,长轴长为
轴上,长轴长为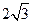 ,离心率为
,离心率为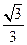 ,经过其左焦点
,经过其左焦点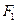 的直线
的直线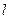 交椭圆
交椭圆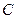 于
于 、
、 两点(I)求椭圆
两点(I)求椭圆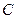 的方程;
的方程;
(II)在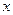 轴上是否存在一点
轴上是否存在一点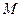 ,使得
,使得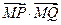 恒为常数?若存在,求出
恒为常数?若存在,求出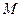 点的坐标和这个常数;若不存在,说明理由.
点的坐标和这个常数;若不存在,说明理由.
(本小题满分14分)
已知椭圆的中心在原点,焦点在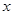 轴上,长轴长是短轴长的2倍,且经过点
轴上,长轴长是短轴长的2倍,且经过点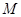 (2,1),平行于
(2,1),平行于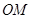 直线
直线 在
在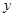 轴上的截距为
轴上的截距为 ,设直线
,设直线 交椭圆于两个不同点
交椭圆于两个不同点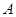 、
、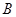 ,
,
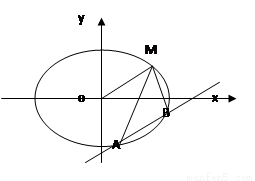
(1)求椭圆方程;
(2)求证:对任意的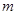 的允许值,
的允许值, 的内心在定直线
的内心在定直线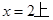 。
。
查看习题详情和答案>>
(本小题满分14分)
已知椭圆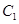 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为 ,
,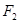
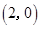 ,点
,点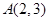 在椭圆
在椭圆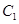 上,过点
上,过点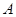 的直线
的直线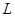 与抛物线
与抛物线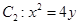 交于
交于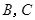 两点,抛物线
两点,抛物线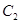 在点
在点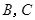 处的切线分别为
处的切线分别为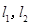 ,且
,且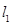 与
与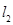 交于点
交于点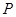 .
.
(1) 求椭圆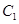 的方程;
的方程;
(2) 是否存在满足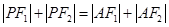 的点
的点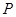 ? 若存在,指出这样的点
? 若存在,指出这样的点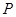 有几个(不必求出点
有几个(不必求出点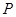 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
查看习题详情和答案>>
.files/image157.gif)
.files/image159.gif)
.files/image112.gif)
.files/image162.gif)
.files/image164.gif)
.files/image166.gif)
.files/image168.gif)
.files/image127.gif)
.files/image170.gif)
.files/image172.gif)
.files/image177.gif)
.files/image135.gif)
.files/image131.gif)
.files/image180.gif)
.files/image182.gif)
.files/image185.gif)
.files/image188.gif)
.files/image190.gif)
.files/image194.gif)
.files/image196.gif)
.files/image198.gif)
.files/image200.gif)
.files/image202.gif)
.files/image206.gif)
.files/image208.gif)
.files/image140.gif)
.files/image212.gif)
.files/image214.gif)
.files/image216.gif)
.files/image218.gif)
.files/image220.gif)
.files/image222.gif)
.files/image224.gif)
.files/image226.gif)
.files/image228.gif)
.files/image230.gif)
.files/image232.gif)
.files/image234.gif)
.files/image236.gif)
.files/image238.gif)
.files/image240.gif)
.files/image242.gif)
.files/image054.gif)
.files/image245.gif)
.files/image247.gif)
.files/image249.gif)
.files/image251.gif)
.files/image253.gif)
.files/image255.gif)
.files/image257.gif)
.files/image259.gif)
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆上的点到
轴上,椭圆上的点到 ,离心率
,离心率 .
. 、
、 ,过点
,过点 的直线
的直线 与该椭圆交于点
与该椭圆交于点 、
、 ,
,  、
、 为邻边作平行四边形
为邻边作平行四边形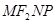 ,求该平行四边形对角线
,求该平行四边形对角线 的长度
的长度
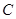 的中心在原点,一个焦点
的中心在原点,一个焦点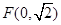 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是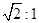 .若椭圆
.若椭圆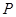 的横坐标为
的横坐标为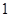 ,过点
,过点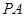 ,
,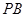 分别交椭圆
分别交椭圆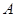 ,
,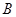 .
.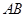 的斜率为定值;
的斜率为定值; 面积的最大值.
面积的最大值.