网址:http://m.1010jiajiao.com/timu_id_24542[举报]
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
B
B
D
B
D
C
A
B
C
A
D
二、填空题
13、(-¥,-1)È(2,+¥) 14 、2n ?
1 15、45 16、 17、0.94 18、
17、0.94 18、
三、解答题
19、解: 设等比数列{an}的公比为q, 则q≠0, a2= = , a4=a3q=2q
所以 + 2q= , 解得q1= , q2= 3,
当q1=, a1=18.所以 an=18×()n-1= = 2×33-n.
当q=3时, a1= , 所以an=×3n-1=2×3n-3
 20、解:(1)将函数解析式变形为
20、解:(1)将函数解析式变形为


 (2)方程f(x)=5的解分别是
和 , 由于f(x)在(-∞,-1]和[2,5]上单调递减,在[-1,2]和[5,+∞)上单调递增,因此
(2)方程f(x)=5的解分别是
和 , 由于f(x)在(-∞,-1]和[2,5]上单调递减,在[-1,2]和[5,+∞)上单调递增,因此
 .
.
 由于
由于
21、解:(1)当a=2时,A=(2,7),B=(4,5)∴ A B=(4,5)
B=(4,5)
(2)∵ B=(
当a< 时,A=(
时,A=( A,必须
A,必须 ,此时a=-1;
,此时a=-1;
当a= 时,A=
时,A= ,使B
,使B A的a不存在;
A的a不存在;
当a> 时,A=(2,
时,A=(2, A,必须
A,必须 ,此时1≤a≤3.
,此时1≤a≤3.
综上可知,使B A的实数a的取值范围为[1,3]∪{-1}
A的实数a的取值范围为[1,3]∪{-1}
22、解:(Ⅰ)求导得 。
。
由于  的图像与直线
的图像与直线 相切于点
相切于点 ,
,
所以 ,即:
,即:
 1
1 .
.
3
(Ⅱ)由 得:
得:
令f′(x)>0,解得 x<-1或x>3;又令f′(x)< 0,解得 -1<x<3.
故当x (
( , -1)时,f(x)是增函数,当 x
, -1)时,f(x)是增函数,当 x (3,
(3, )时,f(x)也是增函数,
)时,f(x)也是增函数,
但当x (-1 ,3)时,f(x)是减函数.
(-1 ,3)时,f(x)是减函数.
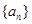 中,若
中,若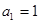 ,
,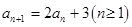 ,则该数列的通项
,则该数列的通项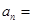 ________________.
________________.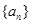 中,若
中,若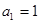 ,
, ,则该数列的通项
,则该数列的通项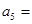 ________________.
________________. 中,若
中,若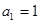 ,
, ,则该数列的通项
,则该数列的通项 ________________.
________________. 中,若
中,若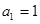 ,
,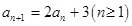 ,则该数列的通项
,则该数列的通项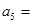 ________________.
________________.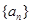 中,若
中,若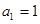 ,
,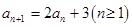 ,则该数列的通项
,则该数列的通项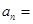 ________________.
________________.