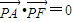摘要:(III)双曲线的左.右焦点分别为的左.右顶点.而的左.右顶点分别是的左.右焦点..若直线与双曲线恒有两个不同的交点和.且(其中为原点). 求的取值范围.本小题涉及直线.圆.椭圆.双曲线.求点的轨迹方程.求方程.求参数的范围等多个知识点.能较全面地考察解析几何的基础知识.知识点的考察面宽.对数学综合能力要求高.可使之成为有较好区分度的试题. 在知识的交汇点处设计试题.将解析几何的各知识点与向量有机地融合在一起.在考查知识的同时.可以较好地考查考生对解析几何基本思想的理解和通性通法的掌握.以及运算能力和运用所学知识分析问题.解决问题的能力.解题思路:第I问可从平面向量数量积的坐标运算入手或数形结合即可得出圆的方程.入手较易,第2问是考查两直线垂直的位置关系以及直线方程的求解方法.只要数形结合.便可由垂径定理得出垂直条件,第3问考察直线和圆锥曲线的位置关系.首先要用待定系数法求出双曲线方程.解题时只要能熟练掌握有关圆锥曲线的基本知识要能将“几何元件 熟练地破译成坐标或代数式的形式.合理运用方程.不等式的知识为工具.
网址:http://m.1010jiajiao.com/timu_id_24160[举报]
点A、B分别是以双曲线
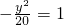 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,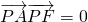
(I)求椭圆C的方程;
(II)求点P的坐标;
(III)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值.
查看习题详情和答案>>
点A、B分别是以双曲线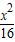
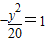 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,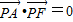
(I)求椭圆C的方程;
(II)求点P的坐标;
(III)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值.
查看习题详情和答案>>
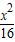
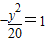 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,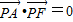
(I)求椭圆C的方程;
(II)求点P的坐标;
(III)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值.
查看习题详情和答案>>
点A、B分别是以双曲线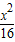
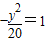 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,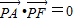
(I)求椭圆C的方程;
(II)求点P的坐标;
(III)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值.
查看习题详情和答案>>
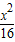
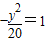 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,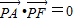
(I)求椭圆C的方程;
(II)求点P的坐标;
(III)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值.
查看习题详情和答案>>
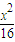
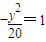 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,