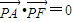题目内容
点A、B分别是以双曲线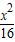
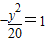 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,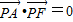
(I)求椭圆C的方程;
(II)求点P的坐标;
(III)设M是椭圆长轴AB上的一点,点M到直线AP的距离等于|MB|,求椭圆上的点到M的距离d的最小值.
【答案】分析:(I)求出双曲线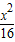
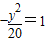 的焦点、顶点,得出椭圆的a,c,b即可求出椭圆标准方程.
的焦点、顶点,得出椭圆的a,c,b即可求出椭圆标准方程.
(Ⅱ)点P的坐标为(x,y),由已知得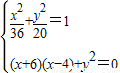 解方程组可得点P的坐标
解方程组可得点P的坐标
(Ⅲ)设点M是(m,0)于是 ,解出m=2,建立椭圆上的点到M的距离d的表达式,用函数知识求最值
,解出m=2,建立椭圆上的点到M的距离d的表达式,用函数知识求最值
解答:解(I)已知双曲线实半轴a1=4,虚半轴b1=2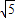 ,半焦距c1=
,半焦距c1=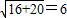 ,
,
∴椭圆的长半轴a2=c1=6,椭圆的半焦距c2=a1=4,椭圆的短半轴b2=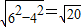 ,
,
∴所求的椭圆方程为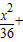
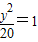
(II)由已知A(-6,0),F(4,0),
设点P的坐标为(x,y),则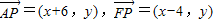 ,由已知得
,由已知得
则2x2+9x-18=0,解之得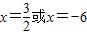 ,
,
由于y>0,所以只能取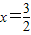 ,于是
,于是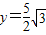 ,所以点P的坐标为
,所以点P的坐标为 (9分)
(9分)
(Ⅲ)直线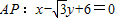 ,设点M是(m,0),则点M到直线AP的距离是
,设点M是(m,0),则点M到直线AP的距离是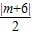 ,于是
,于是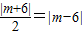 ,
,
又∵点M在椭圆的长轴上,即-6≤m≤6∴m=2
∴当m=2时,椭圆上的点到M(2,0)的距离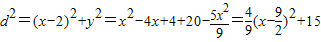
又-6≤x≤6∴当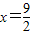 时,d取最小值
时,d取最小值
点评:本题考查圆锥曲线的几何性质、标准方程、距离求解.考查函数知识、方程思想、计算能力.
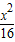
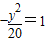 的焦点、顶点,得出椭圆的a,c,b即可求出椭圆标准方程.
的焦点、顶点,得出椭圆的a,c,b即可求出椭圆标准方程.(Ⅱ)点P的坐标为(x,y),由已知得
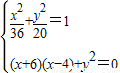 解方程组可得点P的坐标
解方程组可得点P的坐标(Ⅲ)设点M是(m,0)于是
 ,解出m=2,建立椭圆上的点到M的距离d的表达式,用函数知识求最值
,解出m=2,建立椭圆上的点到M的距离d的表达式,用函数知识求最值解答:解(I)已知双曲线实半轴a1=4,虚半轴b1=2
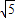 ,半焦距c1=
,半焦距c1=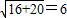 ,
,∴椭圆的长半轴a2=c1=6,椭圆的半焦距c2=a1=4,椭圆的短半轴b2=
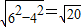 ,
,∴所求的椭圆方程为
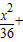
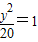
(II)由已知A(-6,0),F(4,0),
设点P的坐标为(x,y),则
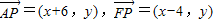 ,由已知得
,由已知得
则2x2+9x-18=0,解之得
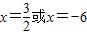 ,
,由于y>0,所以只能取
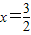 ,于是
,于是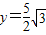 ,所以点P的坐标为
,所以点P的坐标为 (9分)
(9分)(Ⅲ)直线
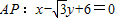 ,设点M是(m,0),则点M到直线AP的距离是
,设点M是(m,0),则点M到直线AP的距离是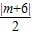 ,于是
,于是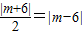 ,
,又∵点M在椭圆的长轴上,即-6≤m≤6∴m=2
∴当m=2时,椭圆上的点到M(2,0)的距离
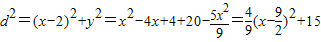
又-6≤x≤6∴当
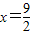 时,d取最小值
时,d取最小值
点评:本题考查圆锥曲线的几何性质、标准方程、距离求解.考查函数知识、方程思想、计算能力.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
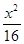
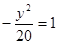 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,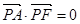

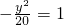 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,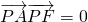
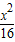
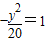 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,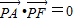
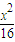
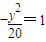 的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,
的焦点为顶点,顶点为焦点的椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆C上,且位于x轴上方,