摘要：又tan∠ADC=2,所以.即DC=BC.(2)等腰三角形.
网址：http://m.1010jiajiao.com/timu_id_23563[举报]
如图，已知二次函数y=ax2+2x+3的图象与x轴交于点A、点B（点B在X轴的正半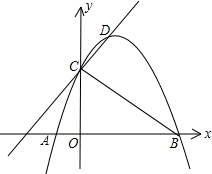
轴上），与y轴交于点C，其顶点为D，直线DC的函数关系式为y=kx+3，又tan∠OBC=1，
（1）求a、k的值；
（2）探究：在该二次函数的图象上是否存在点P（点P与点B、C补重合），使得△PBC是以BC为一条直角边的直角三角形？若存在，求出点P的坐标；若不存在，请你说明理由． 查看习题详情和答案>>
轴上），与y轴交于点C，其顶点为D，直线DC的函数关系式为y=kx+3，又tan∠OBC=1，（1）求a、k的值；
（2）探究：在该二次函数的图象上是否存在点P（点P与点B、C补重合），使得△PBC是以BC为一条直角边的直角三角形？若存在，求出点P的坐标；若不存在，请你说明理由． 查看习题详情和答案>>
已知：如图，AB∥CD，∠ABC=∠ADC，BF、DE分别是∠ABC，∠ADC的角平分线，由此可判断DE∥BF，请在括号内填写合理的理由．
解：∵BF、DE分别是∠ABC，∠ADC的角平分线（已知）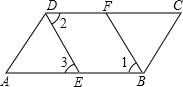
∴∠1=
∠ABC， ∠2=
∠ （角平分线定义）
又∵∠ABC=∠ADC（已知）
∴ = （等量代换）
∵AB∥CD（已知）
∴∠2=∠3
∴∠ =∠ （等量代换 ）
∴DE∥BF ．
查看习题详情和答案>>
解：∵BF、DE分别是∠ABC，∠ADC的角平分线（已知）
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ABC=∠ADC（已知）
∴
∵AB∥CD（已知）
∴∠2=∠3
∴∠
∴DE∥BF
如图，在△ABC中，∠ACB=90°，O为BC边上一点，以O为圆心，OB为半径作半圆与AB边和BC边分别交于点D、点E，连接CD，且CD=CA，BD=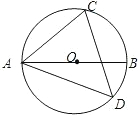
如图AB是⊙O的直径，且AB=10，sin∠BAC=0.6，点D为优弧ABC上任一点．