网址:http://m.1010jiajiao.com/timu_id_233695[举报]
一、.填空题
1.设集合 ,
,  , 则A∩B=
, 则A∩B=
2. 在等比数列 中,
中, ,公比q是整数,则
,公比q是整数,则 = ―128
= ―128
3.
已知0< , 则A与B的大小关系是 A<B
, 则A与B的大小关系是 A<B
4.在数列 中,已知
中,已知 ,当
,当 时,
时, ,那么
,那么
 .
.
5. 正数 满足
满足 ,则
,则 的最小值为
的最小值为 __
__
6. 已知数列 ,
, ,且数列
,且数列 的前
的前 项和为
项和为 ,那么
,那么 的值为______99____
的值为______99____
7. 已知函数 的定义域是R,则实数k的取值范围是 _
的定义域是R,则实数k的取值范围是 _
8. 等差数列的前15项的和为-5,前45项的和为30,则前30项的和为___5_____
9. 已知两个等差数列 的前n项的和分别为
的前n项的和分别为 ,且
,且 ,则
,则  =_
=_ _
_
10.若 是等差数列,首项
是等差数列,首项
 ,
, ,则使前n项和
,则使前n项和 成立的最大正整数n是 4006
成立的最大正整数n是 4006
11.若正数a、b满足ab=a+b+3, 则ab的取值范围是 
12.设 ≥0,
≥0, ≥0,且
≥0,且 ,则
,则 的最大值为____
的最大值为____ __
__
13.不等式 的解集是
的解集是 或
或 __
__
14.若不等式 对满足
对满足 的所有
的所有 都成立,则
都成立,则 的取值范围(
的取值范围( ,
, )_
)_
二.解答题
15.(本题14分)设全集为R,集合A={ ㄏ
ㄏ (3-
(3- )
) },B={
},B={ ㄏ
ㄏ },
},
求 .
.
解:A=[-1,3) ……3分
, B=(-2,3] ……6分
 [-1,3)
……9分
[-1,3)
……9分
 ……14分
……14分
16.(本题14分)设数列 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
.
(1)设 ,求数列
,求数列 的通项公式;
的通项公式;
(2)求数列{ }的通项公式.
}的通项公式.
解:(1)依题意, ,即
,即 , ……3分
, ……3分
由此得 .
……6分
.
……6分
因此,所求通项公式为
 ,
, .
……8分
.
……8分
(2)由①知 ,
, ,
,
于是,当 时,
时,


 ,
……12分
,
……12分
 13分
13分
 ……14分
……14分
17.(本题15分)已知二次函数 的二次项系数为
的二次项系数为 ,且不等式
,且不等式 的解集为
的解集为 .
.
(1)若方程 有两个相等的根,求
有两个相等的根,求 的解析式;
的解析式;
(2)若 的最大值为正数,求
的最大值为正数,求 的取值范围.
的取值范围.
解:(1)设 由
由 得
得
它的解集为(1,3)得方程 的两根为1和3且a<0
的两根为1和3且a<0
 即
即 ……(1)
……3分
……(1)
……3分
 有等根得
有等根得
 ……(2)
……6分
……(2)
……6分
由(1)(2)及 得
得
故 的解析式为
的解析式为 ……8分
……8分
(2)由
及 ……10分
……10分
由 ……12分
……12分
解得  ……15分
……15分
18.(本题15分)已知
 , 若
, 若 在区间
在区间 上的最大值为
上的最大值为 , 最小值为
, 最小值为 , 令
, 令 .
.
(1) 求 的函数表达式;
的函数表达式;
(2) 判断 的单调性, 并求出
的单调性, 并求出 的最小值.
的最小值.
解:(1) 函数 的对称轴为直线
的对称轴为直线 , 而
, 而
∴ 在
在 上
上 ……3分
……3分
①当 时,即
时,即 时,
时, ……5分
……5分
②当2 时,即
时,即 时,
时, ……7分
……7分
 ……8分
……8分
(2)
 .
……15分
.
……15分
19.(本题16分)某房地产开发公司计划在一楼区内建造一个长方形公园 ,公园由长方形的休闲区
,公园由长方形的休闲区 和环公园人行道(阴影部分)组成.已知休闲区
和环公园人行道(阴影部分)组成.已知休闲区 的面积为
的面积为 平方米,人行道的宽分别为
平方米,人行道的宽分别为 米和
米和 米(如图)
米(如图)
(1)若设休闲区的长和宽的比 ,求公园
,求公园 所占面积
所占面积 关于
关于 的函数
的函数 的解析式;
的解析式;
 (2)要使公园所占面积最小,休闲区
(2)要使公园所占面积最小,休闲区 的长和宽该如何设计?
的长和宽该如何设计?
解:(1)设休闲区的宽为 米,则其长为
米,则其长为 米,
米,
∴ ,
,
∴
 …8分
…8分
(2)
 ,当且仅当
,当且仅当 时,公园所占面积最小,
……14分
时,公园所占面积最小,
……14分
此时, ,即休闲区
,即休闲区 的长为
的长为 米,宽为
米,宽为 米。……16分
米。……16分
20.已知函数 满足
满足 .
.
(1)求 的值;
的值;
(2)若数列
 ,求数列
,求数列 的通项公式;
的通项公式;
(3)若数列 满足
满足 ,
, 是数列
是数列 前
前 项的和,是否存在正实数
项的和,是否存在正实数 ,使不等式
,使不等式 对于一切的
对于一切的 恒成立?若存在指出
恒成立?若存在指出 的取值范围,并证明;若不存在说明理由.
的取值范围,并证明;若不存在说明理由.
解:(1)令 ,
, ,
, ,
……2分
,
……2分
令 ,
, ……5分
……5分
(2)∵ ①
①
∴ ②
②
由(Ⅰ),知 
∴①+②,得 …… 10分
…… 10分
(3)∵  ,∴
,∴ 
∴ , ①
, ①
 ,
②
,
②
①-②得
即 …… 12分
…… 12分
要使得不等式 恒成立,即
恒成立,即 对于一切的
对于一切的 恒成立,
恒成立,

设
当 时,由于对称轴直线
时,由于对称轴直线 ,且
,且  ,而函数
,而函数 在
在 是增函数,∴不等式
是增函数,∴不等式 恒成立
恒成立
即当实数 大于
大于 时,不等式
时,不等式 对于一切的
对于一切的 恒成立 ……16分
恒成立 ……16分
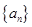 中,
中,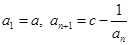 .
.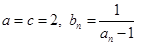 ,求数列
,求数列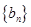 的通项公式;
的通项公式;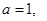 求证:
求证: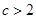 .
.
 中,
中, .
. ,求数列
,求数列 的通项公式;
的通项公式; 求证:
求证: .
. 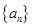 中,
中,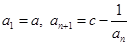 .
.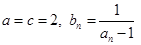 ,求数列
,求数列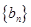 的通项公式;
的通项公式;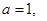 求证:
求证: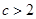 .
.