网址:http://m.1010jiajiao.com/timu_id_22965[举报]
一 、选择题
1.C. 2.A. 3.A. 4.A. 5.A. 6.C. 7.A. 8.A. 9.C. 10.D. 11.C.12.D.
一、 填空题
13. . 14.2. 15.16. 16.13.
. 14.2. 15.16. 16.13.
三、解答题
17.(理科) (1)由(1+tanA)(1+tanB)=2,得
tanA+tanB=1-tanAtanB,
即tan(A+B)=1.
∵A、B为△ABC内角, ∴A+B= . 则 C=
. 则 C= (定值).
(定值).
(2)已知△ABC内接于单位圆, ∴△ABC外接圆半径R=1.
∴由正弦定理得: ,
, ,
, .
.
则△ABC面积S= =
= =
=
= =
=
= =
= .
.
∵ 0<B< , ∴
, ∴ .
.
故 当 时,△ABC面积S的最大值为
时,△ABC面积S的最大值为 .
.
(文科) (1) ,
,
 ,
, ,
, ,∴
,∴  .
.
∴ 向量 和
和 的夹角
的夹角 的大小为
的大小为 .
.
(2) .
.
以 和
和 为邻边的平行四边形的面积
为邻边的平行四边形的面积 ,
,
据此猜想, 的几何意义是以
的几何意义是以 、
、 为邻边的平行四边形的面积.
为邻边的平行四边形的面积.
18. (1)学生甲恰好抽到3道历史题,2道地理题的概率为
 .
.
(2)若学生甲被评为良好,则他应答对5道题或4道题
而答对4道题包括两种情况:①答对3道历史题和1道地理(错一道地理题);②答对2道历史题和2道地理题(错一道历史题)。
设答对5道记作事件A;
答对3道历史题,1道地理题记作事件B;
答对2道历史题,2道地理题,记作事件C;
 ,
,
 ,
,
 .
.
∴甲被评为良好的概率为:
 .
.
19. (1)延长AC到G,使CG=AC,连结BG、DG,E是AB中点, .
.
故直线BG和BD所成的锐角(或直角)就是CE和BD所成的角.

(2)设C到平面ABD的距离为h


20. (1) .
.
(2) 由(1)知: ,故
,故 在
在 是增函数.
是增函数.
又 对于一切
对于一切 恒成立.
恒成立.
由定理知:存在
由(1)知: 

由 的一般性知:
的一般性知: .
.
21. (1)以 中点
中点 为原点,
为原点, 所在直线为
所在直线为 轴,建立平面直角坐标系,则
轴,建立平面直角坐标系,则 .
.
 |
设 ,由
,由 得
得 ,此即点
,此即点 的轨迹方程.
的轨迹方程.
(2)将 向右平移一个单位,再向下平移一个单位后,得到圆
向右平移一个单位,再向下平移一个单位后,得到圆 ,
,
依题意有 .
.
(3)不妨设点 在
在 的上方,并设
的上方,并设 ,则
,则 ,
,
所以 ,由于
,由于 且
且 ,
,
故 .
.
22.(理科)⑴ ∵f(x)+g(x)=ax,∴f(-x)+ g(-x)=a-x.
∵f(x)是奇函数,g(x)是偶函数,∴-f(x)+g(x)=a-x .
∴f(x)= ,g(x)=
,g(x)= .
.
⑵
 是R上的减函数,
是R上的减函数,
∴y=f -1(x)也是R上的减函数.
又

⑶



 n>2,
n>2, 当
当 上是增函数.
上是增函数. 是减函数;
是减函数;
 上是减函数.
上是减函数. 是增函数.
是增函数.
(文科) (1)∵函数 在
在 和
和 时取得极值,∴-1,3是方程
时取得极值,∴-1,3是方程 的两根,
的两根,
∴
(2) ,当x变化时,有下表
,当x变化时,有下表
x
(-∞,-1)
-1
(-1,3)
3
(3,+∞)
f’(x)
+
0
-
0
+
f(x)
ㄊ
Max
c+5
ㄋ
Min
c-27
ㄊ
而 时f(x)的最大值为c+54.
时f(x)的最大值为c+54.
要使f(x)<2|c|恒成立,只要c+54<2|c|即可.
当c≥0时c+54<
当c<0时c+54<-
∴c∈(-∞,-18)∪(54,+∞).
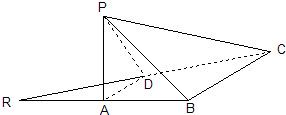 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2.点A、D分别是RB、RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连接PB、PC.(1)求证:PB⊥BC;
(2)在线段PB上找一点E,使AE∥平面PCD;
(3)求二面角A-CD-P的余弦值. 查看习题详情和答案>>
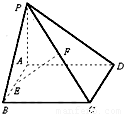
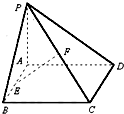 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E、F分别是AB、PC的中点.(1)求证:EF∥平面PAD;
(2)求证:CD⊥EF
(3)求EF与平面ABCD所成的角的大小.
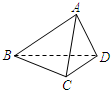
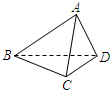 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.(1)求证:AD⊥BC;
(2)已知点E是CD的中点,点P在△ABC的内部及边界上运动,且满足EP∥平面ABD,试求点P的轨迹;
(3)有一个小虫从点A开始按以下规则前进:在每一个顶点处等可能地选择通过这个顶点的三条棱之一,并且沿着这条棱爬到尽头,当它爬了12cm之后,求恰好回到A点的概率.