题目内容
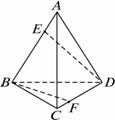
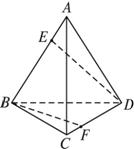
如图,已知正四面体ABCD的棱长为3cm.
(1)求证:AD⊥BC;
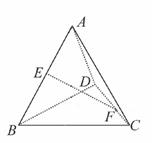
(2)已知点E是CD的中点,点P在△ABC的内部及边界上运动,且满足EP∥平面ABD,试求点P的轨迹;
(3)有一个小虫从点A开始按以下规则前进:在每一个顶点处等可能地选择通过这个顶点的三条棱之一,并且沿着这条棱爬到尽头,当它爬了12cm之后,求恰好回到A点的概率.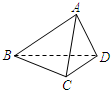
(1)求证:AD⊥BC;
(2)已知点E是CD的中点,点P在△ABC的内部及边界上运动,且满足EP∥平面ABD,试求点P的轨迹;
(3)有一个小虫从点A开始按以下规则前进:在每一个顶点处等可能地选择通过这个顶点的三条棱之一,并且沿着这条棱爬到尽头,当它爬了12cm之后,求恰好回到A点的概率.

(1)证明:取BC中点M,连AM、DM,
因△ABC及△BCD均为正三角形,故BC⊥AM,BC⊥DM.
因AM,DM为平面ADM内的两条相交直线,
故BC⊥平面ADM,于是BC⊥AD.
(2)连接EM,并取AC的中点Q,连QE,QM.于是EQ∥AD,故EQ∥平面ABD.
同理MQ∥平面ABD.
因EQ,MQ为平面QEM内的两条相交直线,
故平面QEM∥平面ABD,从而点P的轨迹为线段QM.
(3)依题设小虫共走过了4条棱,每次走某条棱均有3种选择,
故所有等可能基本事件总数为34=81.
走第1条棱时,有3种选择,不妨设走了AB,然后走第2条棱为:或BA或BC或BD.
若第2条棱走的为BA,则第3条棱可以选择走AB,AC,AD,计3种可能;
若第2条棱走的为BC,则第3条棱可以选择走CB,CD,计2种可能;
同理第2条棱走BD时,第3棱的走法亦有2种选择.
故小虫走12cm后仍回到A点的选择有3×(3+2+2)=21种可能.
于是,所求的概率为
=
.
因△ABC及△BCD均为正三角形,故BC⊥AM,BC⊥DM.
因AM,DM为平面ADM内的两条相交直线,
故BC⊥平面ADM,于是BC⊥AD.
(2)连接EM,并取AC的中点Q,连QE,QM.于是EQ∥AD,故EQ∥平面ABD.
同理MQ∥平面ABD.
因EQ,MQ为平面QEM内的两条相交直线,
故平面QEM∥平面ABD,从而点P的轨迹为线段QM.
(3)依题设小虫共走过了4条棱,每次走某条棱均有3种选择,
故所有等可能基本事件总数为34=81.
走第1条棱时,有3种选择,不妨设走了AB,然后走第2条棱为:或BA或BC或BD.
若第2条棱走的为BA,则第3条棱可以选择走AB,AC,AD,计3种可能;
若第2条棱走的为BC,则第3条棱可以选择走CB,CD,计2种可能;
同理第2条棱走BD时,第3棱的走法亦有2种选择.
故小虫走12cm后仍回到A点的选择有3×(3+2+2)=21种可能.
于是,所求的概率为
| 21 |
| 81 |
| 7 |
| 27 |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
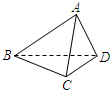 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.