摘要：故存在一个实数=-1.使得数列{}为等差数列. --------5分
网址：http://m.1010jiajiao.com/timu_id_221682[举报]
已知数列{an}满足an=2an-1+2n+2（n≥2），a1=2．
（1）是否存在一个实数t，使得数列{
}成等差数列，若存在，求出t的值；若不存在，请说明理由；
（2）设数列{an}的前n项和为Sn，判断Sn与n3+n2的大小，并说明理由． 查看习题详情和答案>>
（1）是否存在一个实数t，使得数列{
| an+t | 2n |
（2）设数列{an}的前n项和为Sn，判断Sn与n3+n2的大小，并说明理由． 查看习题详情和答案>>
已知数列{an}满足an=2an-1+2n+2（n≥2），a1=2．
（1）是否存在一个实数t，使得数列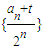
成等差数列，若存在，求出t的值；若不存在，请说明理由；
（2）设数列{an}的前n项和为Sn，判断Sn与n3+n2的大小，并说明理由．
查看习题详情和答案>>
（1）是否存在一个实数t，使得数列
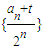成等差数列，若存在，求出t的值；若不存在，请说明理由；（2）设数列{an}的前n项和为Sn，判断Sn与n3+n2的大小，并说明理由．
查看习题详情和答案>>
（2004•虹口区一模）数列{an}满足an=3an-1+3n-1 （n≥2），且a3=95．
（1）求a1，a2；
（2）是否存在一个实数t，使得bn=
(an+t)（n∈Z+），{bn}为等差数列．有，则求出t，并予以证明；没有，则说明理由；
（3）求数列{an}的前n项和Sn．
查看习题详情和答案>>
（1）求a1，a2；
（2）是否存在一个实数t，使得bn=
| 1 | 3n |
（3）求数列{an}的前n项和Sn．
（2006•石景山区一模）已知函数y=f（x）对于任意θ≠
（k∈Z），都有式子f（a-tanθ）=cotθ-1成立（其中a为常数）．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）利用函数y=f（x）构造一个数列，方法如下：
对于给定的定义域中的x1，令x2=f（x1），x3=f（x2），…，xn=f（xn-1），…在上述构造过程中，如果xi（i=1，2，3，…）在定义域中，那么构造数列的过程继续下去；如果xi不在定义域中，那么构造数列的过程就停止．
（ⅰ）如果可以用上述方法构造出一个常数列，求a的取值范围；
（ⅱ）是否存在一个实数a，使得取定义域中的任一值作为x1，都可用上述方法构造出一个无穷数列{xn}？若存在，求出a的值；若不存在，请说明理由；
（ⅲ）当a=1时，若x1=-1，求数列{xn}的通项公式．
查看习题详情和答案>>
| kπ | 2 |
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）利用函数y=f（x）构造一个数列，方法如下：
对于给定的定义域中的x1，令x2=f（x1），x3=f（x2），…，xn=f（xn-1），…在上述构造过程中，如果xi（i=1，2，3，…）在定义域中，那么构造数列的过程继续下去；如果xi不在定义域中，那么构造数列的过程就停止．
（ⅰ）如果可以用上述方法构造出一个常数列，求a的取值范围；
（ⅱ）是否存在一个实数a，使得取定义域中的任一值作为x1，都可用上述方法构造出一个无穷数列{xn}？若存在，求出a的值；若不存在，请说明理由；
（ⅲ）当a=1时，若x1=-1，求数列{xn}的通项公式．