网址:http://m.1010jiajiao.com/timu_id_211198[举报]
一、ACBCD DDCAB
二、11。 12。12
13。
12。12
13。
14。


15。②③⑤
三、16解:(I)


 。。。。。。。。。。。。。。。。。。。 4分
。。。。。。。。。。。。。。。。。。。 4分
 。。。。。。。。。。。。。。。。。。。 6分
。。。。。。。。。。。。。。。。。。。 6分
(II)
 。。。。。。。。。。。。。。。。。。。 8分
。。。。。。。。。。。。。。。。。。。 8分
 。。。。。。。。。。。。。。。。。。。. 9分
。。。。。。。。。。。。。。。。。。。. 9分
 。。。。。。。。。。。。。。。。。。。. 12分
。。。。。。。。。。。。。。。。。。。. 12分
当 。。。。。。。。。。。。。。 13分
。。。。。。。。。。。。。。 13分
17解(1)连接B
∵D为AC中点 ∴OD∥B
又B 平面BDC1,OD
平面BDC1,OD 平面BDC1
平面BDC1
∴B
(2)∵AA1⊥面ABC,BC⊥AC,AA1∥CC1
∴CC1⊥面ABC 则BC⊥平面AC1,CC1⊥AC
如图以C为坐标原点,CA所在直线为X轴,CB所在直线为Y轴, 所在直线为
所在直线为 轴建立空间直角坐标系 则C1(0,0,3) B(0,2,0) D(1,0,0) C(0,0,0) 。。。。。。。。。。。。。。。。。 8分
轴建立空间直角坐标系 则C1(0,0,3) B(0,2,0) D(1,0,0) C(0,0,0) 。。。。。。。。。。。。。。。。。 8分
∴设平面 的法向量为
的法向量为 由
由 得
得
 ,取
,取 , 则
, 则 。。。。。。。。。10分
。。。。。。。。。10分
又平面BDC的法向量为 。。。。。。。。。。。。。。。。。。。 11分
。。。。。。。。。。。。。。。。。。。 11分
cos
∴二面角C1―BD―C的余弦值为 。。。。。。。。。13分
。。。。。。。。。13分
18解:(I)设周五有语文、数学、外语三科作业分别为事件A1、A2、A3周五没有语文、数学、外语三科作业为事件A,则由已知表格得
 、
、 、
、 。。。。。。。。。。。。2分
。。。。。。。。。。。。2分

 。。。。。。。。。。4分
。。。。。。。。。。4分
(II)设一周内有数学作业的天数为 ,则
,则





 。。。。。。。。。。。。。。。。。。。。。10分
。。。。。。。。。。。。。。。。。。。。。10分
所以随机变量 的概率分布列如下:
的概率分布列如下:

0
1
2
3
4
5
P






故 。。。。。。。。。。13分
。。。。。。。。。。13分
19解:(Ⅰ)由题意,可设抛物线方程为 .
.
由 ,得
,得 .
. 抛物线的焦点为
抛物线的焦点为 ,
, .
.
 抛物线D的方程为
抛物线D的方程为 . 。。。。。。。。。。。。。。。。。。。。。。。4分
. 。。。。。。。。。。。。。。。。。。。。。。。4分
(Ⅱ)设A 由于O为PQ之中点,故当
由于O为PQ之中点,故当 轴时由抛物线的对称性知
轴时由抛物线的对称性知 。。。。。。。。。。。。。。。。。。
。。。。。。。。。。。。。。。。。。
当 不垂直
不垂直 轴时,设
轴时,设 :
: ,
,
由
 ,
,
 ,
, ,
,
 …
…



(Ⅲ)设存在直线 满足题意,则圆心
满足题意,则圆心 ,过M作直线
,过M作直线 的垂线,
的垂线,
垂足为E, 设直线 与圆交于点
与圆交于点 ,可得,
,可得,
即  =
=
=
= =
=

当 时,
时, ,此时直线
,此时直线 被以AP为直径的圆截得的弦长恒为定值
被以AP为直径的圆截得的弦长恒为定值 .…12分
.…12分
因此存在直线 满足题意.
……13分
满足题意.
……13分
20解:(Ⅰ) 
 ,
,
 . 。。。。。。。。。。。。。。。。。。2分
. 。。。。。。。。。。。。。。。。。。2分
当 时,
时, . 。。。。。。。。。。。。。。。。。。。。。。。。。。3分
. 。。。。。。。。。。。。。。。。。。。。。。。。。。3分
 当
当 时,
时, ,此时函数
,此时函数 递减;
递减;
当 时,
时, ,此时函数
,此时函数 递增;
递增;
∴当 时,
时, 取极小值,其极小值为
取极小值,其极小值为 . 。。。。。。。。。。。。。。。。。。6分
. 。。。。。。。。。。。。。。。。。。6分
(Ⅱ)解法一:由(Ⅰ)可知函数 和
和 的图像在
的图像在 处有公共点,因此若存在
处有公共点,因此若存在 和
和 的隔离直线,则该直线过这个公共点. 。。。。。。。。。。。。。。。。。。。。。。。7分
的隔离直线,则该直线过这个公共点. 。。。。。。。。。。。。。。。。。。。。。。。7分
设隔离直线的斜率为 ,则直线方程为
,则直线方程为 ,
,
即  .。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
由 ,可得
,可得 当
当 时恒成立.
时恒成立.
 ,
,  由
由 ,得
,得 .。。。。。。。。。。。。。。。。。10分
.。。。。。。。。。。。。。。。。。10分
下面证明 当
当 时恒成立.
时恒成立.
令
 ,则
,则
 , 。。。。。。。。。。。。。。。。。。。。。。11分
, 。。。。。。。。。。。。。。。。。。。。。。11分
当 时,
时, .
.
 当
当 时,
时, ,此时函数
,此时函数 递增;
递增;
当 时,
时, ,此时函数
,此时函数 递减;
递减;
∴ 当 时,
时, 取极大值,也是最大值,其最大值为
取极大值,也是最大值,其最大值为 .
.
从而 ,即
,即 恒成立.。。。。。。。13分
恒成立.。。。。。。。13分
∴ 函数 和
和 存在唯一的隔离直线
存在唯一的隔离直线 .。。。。。。。。。。。。。。。14分
.。。。。。。。。。。。。。。。14分
解法二:
由(Ⅰ)可知当 时,
时, (当且当
(当且当 时取等号) .。。。。。7分
时取等号) .。。。。。7分
若存在 和
和 的隔离直线,则存在实常数
的隔离直线,则存在实常数 和
和 ,使得
,使得
 和
和 恒成立,
恒成立,
令 ,则
,则 且
且
 ,即
,即 . 。。。。。。。。。。。。。。。。。。。。。。。。8分
. 。。。。。。。。。。。。。。。。。。。。。。。。8分
后面解题步骤同解法一.
21(!)解:PQ= ,
,
PQ矩阵表示的变换T: 满足条件
满足条件
 . 所以
. 所以 。。。。。。。。。。。。。。。。。。(3分)
。。。。。。。。。。。。。。。。。。(3分)
直线 任取点
任取点 ,则点
,则点 在直线
在直线 上,
上,
故 ,又
,又 ,得
,得 所以
所以 。。。。。(7分)
。。。。。(7分)
(2) (Ⅰ)曲线C的极坐标方程是 化为直角坐标方程为:
化为直角坐标方程为:
 直线
直线 的直角坐标方程为:
的直角坐标方程为: 。。。。。。。。。3分
。。。。。。。。。3分
(Ⅱ)(法一)由(1)知:圆心的坐标为(2,0),圆的半径R=2,
 圆心到直线l的距离
圆心到直线l的距离



 或
或 。。。。。。。。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。。。。。。。。7分
(法二)把 (
( 是参数)代入方程
是参数)代入方程 ,
,
得 ,
,
 .
.



 或
或 。。。。。。。。。。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。。。。。。。。。。7分
(3) 解:(Ⅰ)


函数 如图所示。。。。。。。。。。。。。3分
如图所示。。。。。。。。。。。。。3分
(Ⅱ)由题设知:
如图,在同一坐标系中作出函数 的图象
的图象
(如图所示)
又解集为 .
.
由题设知,当 或
或 时,
时, 且
且 即
即
由 得:
得:
 。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。7分
若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其定义域上的任意实数
对其定义域上的任意实数![]() 分别满足:
分别满足:![]() 和
和![]() ,则称直线
,则称直线![]()
![]() 为
为![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求![]() 的极值;
的极值;
(Ⅱ) 函数![]() 和
和![]() 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求 的极值;
的极值;
(Ⅱ)函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
查看习题详情和答案>>
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: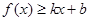 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求 的极值;
的极值;
(Ⅱ)函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
 和
和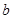 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: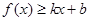 和
和 ,则称直线
,则称直线 为
为 ,
, 为自然对数的底数).
为自然对数的底数). 的极值;
的极值;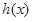 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.