摘要:19.如图.P是边长为1的正六边形ABCDEF所在平面外一点.PA=1.P在平面ABC内的射影为BF的中点O.(Ⅰ)证明PA⊥BF,(Ⅱ)求面APB与面DPB所成二面角的大小.
网址:http://m.1010jiajiao.com/timu_id_21112[举报]
(本题满分12分)
如图,正四棱锥S-ABCD 的底面是边长为 正方形,
正方形, 为底面
为底面
对角线交点,侧棱长是底面边长的 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.

(Ⅰ)求证:AC⊥SD
(Ⅱ)若SD⊥平面PAC, 为
为 中点,求证:
中点,求证: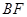 ∥平面PAC;
∥平面PAC;
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 使得BE∥平面PAC.若存在,求SE:EC的值;若不存在,试说明理由。
查看习题详情和答案>>
(本题满分12分)
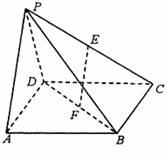 如图,三棱锥P—ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD
如图,三棱锥P—ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD![]()
(1)求证:EF//平面PAD;
(2)求三棱锥C—PBD的体积.
查看习题详情和答案>>(本题满分12分)
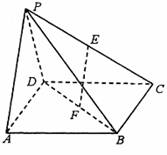 如图,三棱锥P—ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD
如图,三棱锥P—ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD![]()
(1)求证:EF//平面PAD;
(2)求三棱锥C—PBD的体积.
查看习题详情和答案>> ,试将四边形OPDC的面积y表示成
,试将四边形OPDC的面积y表示成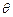 的函数;
的函数;
 的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.