摘要：的条件下.若令.
网址：http://m.1010jiajiao.com/timu_id_206875[举报]
已知数列{an}中，a1=3，a2=5，其前n项和Sn满足Sn+Sn-2=2Sn-1+2n-1（n≥3）．令bn=
．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若f（x）=2x-1，求证：Tn=b1f(1)+b2f(2)+…+bnf(n)＜
（n≥1）；
（Ⅲ）令Tn=
(b1a+b2a2+b3a3+…+bnan)（a＞0），求同时满足下列两个条件的所有a的值：①对于任意正整数n，都有Tn＜
；②对于任意的m∈(0，
)，均存在n0∈N*，使得n≥n0时，Tn＞m．
查看习题详情和答案>>
| 1 |
| an•an+1 |
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若f（x）=2x-1，求证：Tn=b1f(1)+b2f(2)+…+bnf(n)＜
| 1 |
| 6 |
（Ⅲ）令Tn=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
对于函数f（x），若存在x0∈R，使f（x0）=x0成立，则称x0为函数f（x）的不动点，已知f（x）=ax2+（b+1）x+（b-1）（a≠0）
（1）当a=1，b=-2求函数f（x）的不动点；
（2）若对任意实数b，函数f（x）恒有两个相异不动点，求a的取值范围；
（3）在（2）的条件下，令g(x)=
+loga
，解关于x的不等式g[x(x-
)]＜
．
查看习题详情和答案>>
（1）当a=1，b=-2求函数f（x）的不动点；
（2）若对任意实数b，函数f（x）恒有两个相异不动点，求a的取值范围；
（3）在（2）的条件下，令g(x)=
| 1 |
| x+2 |
| 1+x |
| 1-x |
| 1 |
| 2 |
| 1 |
| 2 |
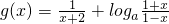，解关于x的不等式
．
。
；
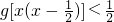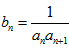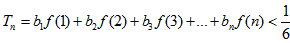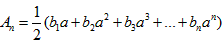（a>0），问是否存在正实数a同时满足下列两个条件？
；
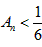），均存在n0∈N，使得当n≥n0时总有An>m，若存在，求出所有的a，若不存在，请说明理由。