题目内容
已知数列{an}中,a1=3,a2=5,其前n项和满足:Sn+Sn-2=2Sn-1+2n-1(n≥3),令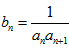 。
。
(1)求数列{an}的通项公式;
(2)若f(x)=2x-1,求证: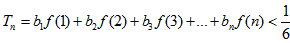 ;
;
(3)令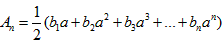 (a>0),问是否存在正实数a同时满足下列两个条件?
(a>0),问是否存在正实数a同时满足下列两个条件?
①对任意n∈N+,都有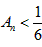 ;
;
②对任意的m∈(0, ),均存在n0∈N,使得当n≥n0时总有An>m,若存在,求出所有的a,若不存在,请说明理由。
),均存在n0∈N,使得当n≥n0时总有An>m,若存在,求出所有的a,若不存在,请说明理由。
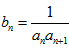 。
。(1)求数列{an}的通项公式;
(2)若f(x)=2x-1,求证:
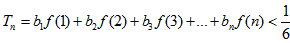 ;
;(3)令
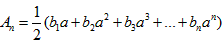 (a>0),问是否存在正实数a同时满足下列两个条件?
(a>0),问是否存在正实数a同时满足下列两个条件?①对任意n∈N+,都有
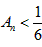 ;
;②对任意的m∈(0,
 ),均存在n0∈N,使得当n≥n0时总有An>m,若存在,求出所有的a,若不存在,请说明理由。
),均存在n0∈N,使得当n≥n0时总有An>m,若存在,求出所有的a,若不存在,请说明理由。 解:(1)由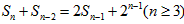 得
得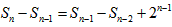 ,
,
即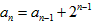 ,移项得
,移项得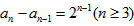 ,
,
∴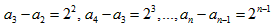 ,这个n-2等式叠加可得,
,这个n-2等式叠加可得,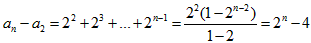
又a2=5,
∴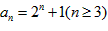 ,经验证
,经验证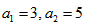 也适合该式,故
也适合该式,故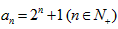 ;
;
(2)由(1)知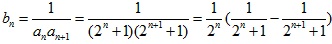 ,
,
又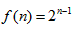 ,
,
∴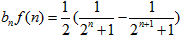
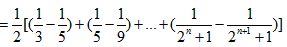 ,
,
故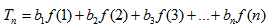 ,
,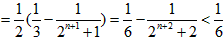 得证;
得证;
(3)由a>0且根据第(2)问的启示,下面a对分三种情况讨论:
1)当a=2时,由(2)知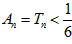 ,满足条件①,
,满足条件①,
另一方面,假设存在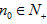 ,使得当
,使得当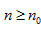 时
时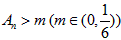 成立,
成立,
即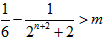 成立,由此解得
成立,由此解得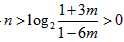 ,设
,设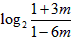 的整数部分为A,
的整数部分为A,
取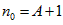 ,则当
,则当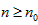 时必有
时必有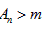 成立,满足条件②,故a=2时符合题意;
成立,满足条件②,故a=2时符合题意;
2)当a>2时,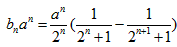 ,由a>2得
,由a>2得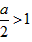 ,
,
∴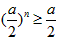 (当n=1时取“=”),
(当n=1时取“=”),
∴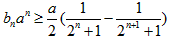 ,
,
∴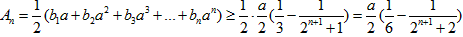 ,
,
令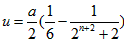 ,由(2)知,当
,由(2)知,当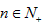 时
时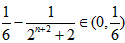 ,
,
∴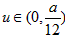 ,
,
又a>2,
∴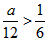 ,在区间
,在区间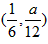 内取一个实数B,必存在一个
内取一个实数B,必存在一个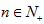 ,使得
,使得 ,这时已不满足条件①,
,这时已不满足条件①,
故a>2时不符合题意,
3)当0<a<2时, 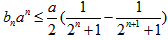 ,
,
∴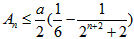 ,
,
由2)知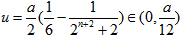 ,即
,即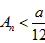 ,
,
而此时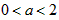 ,
,
∴ ,在区间
,在区间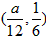 内取一个实数C,这时不存在
内取一个实数C,这时不存在 使得
使得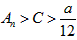 ,否则与
,否则与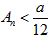 矛盾,此时不满足条件②,
矛盾,此时不满足条件②,
故0<a<2时不符合题意,
综合1), 2), 3)可知,存在正实数a=2符合题意。

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|