网址:http://m.1010jiajiao.com/timu_id_20586[举报]
说明
1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精进行评分。
2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分。
一、(第1题到第12题)
(1)p (2)(理工农医类).files\image037.gif) (3)-49 (4)
(3)-49 (4)(理工农医类).files\image039.gif)
(5)arctg2 (6)[1,3] (7)(理工农医类).files\image041.gif) (8)
(8)(理工农医类).files\image043.gif) (a1>0,0<q<1的一组数)
(a1>0,0<q<1的一组数)
(9)(理工农医类).files\image045.gif) (10)2.6 (11)4p (12)|PF2|=17
(10)2.6 (11)4p (12)|PF2|=17
二、(第13题至第16题)
(13)C (14)D (15)D (16)B
三、(第17题至第22题)
(17)[解] |z1?z2| = |1+sinq cosq +(cosq-sinq )i|
(理工农医类).files\image047.gif)
(理工农医类).files\image049.gif)
故|z1?z2|的最大值为(理工农医类).files\image051.gif) ,最小值为
,最小值为(理工农医类).files\image053.gif) .
.
(理工农医类).files\image054.jpg) (18)[解]连结BC,因为B1B⊥平面ABCD,B1D⊥BC,所以BC⊥BD.
(18)[解]连结BC,因为B1B⊥平面ABCD,B1D⊥BC,所以BC⊥BD.
在△BCD中,BC=2,CD=4,
所以(理工农医类).files\image056.gif)
又因为直线B1D与平面ABCD所成的角等于30°,所以∠B1DB=30°,于是(理工农医类).files\image058.gif)
故平行六面体ABCD-A1B1C1D1的体积为(理工农医类).files\image060.gif)
(19)[解](1)(理工农医类).files\image062.gif)
(理工农医类).files\image064.gif)
(2)归纳概括的结论为:
若数列{an}是首项为a1,公比为q的等比数列,则
(理工农医类).files\image066.gif) ,n为整数.
,n为整数.
证明:(理工农医类).files\image068.gif)
(理工农医类).files\image070.gif)
(理工农医类).files\image072.gif)
(20)[解](1)如图建立直角坐标系,则点p(11,4.5),
(理工农医类).files\image073.jpg) 椭圆方程为
椭圆方程为(理工农医类).files\image075.gif)
将b=h=6与点p坐标代入椭圆方程,得(理工农医类).files\image077.gif) ,此时
,此时(理工农医类).files\image079.gif)
因此隧道的拱宽约为33.3米.
(2)由椭圆方程(理工农医类).files\image081.gif)
得 (理工农医类).files\image083.gif)
因为(理工农医类).files\image085.gif) 即ab≥99,且l=2a,h=b,
即ab≥99,且l=2a,h=b,
所以
(理工农医类).files\image087.gif)
当S取最小值时,有(理工农医类).files\image081.gif) ,得
,得(理工农医类).files\image089.gif)
故当拱高约为6.4米、拱宽约为31.1米,土方工程量最小.
[解二]由椭圆方程(理工农医类).files\image081.gif) 得
得(理工农医类).files\image083.gif)
于是(理工农医类).files\image091.gif)
(理工农医类).files\image093.gif)
即ab≥99,当S取最小值时,有(理工农医类).files\image095.gif)
得(理工农医类).files\image089.gif) 以下同解一.
以下同解一.
(21)[解](1)设(理工农医类).files\image097.gif) ,则由
,则由(理工农医类).files\image099.gif) 即
即(理工农医类).files\image101.gif) 得
得
(理工农医类).files\image103.gif) 或
或(理工农医类).files\image105.gif) 因为
因为(理工农医类).files\image107.gif)
所以 v-3>0,得 v=8,故 (理工农医类).files\image109.gif)
(2)由(理工农医类).files\image111.gif) 得B(10,5),于是直线OB方程:
得B(10,5),于是直线OB方程:(理工农医类).files\image113.gif)
由条件可知圆的标准方程为:(x-3)2+(y+1)2=10,
得圆心(3,-1),半径为(理工农医类).files\image115.gif)
设圆心(3,-1)关于直线OB的对称点为(x,y),则
(理工农医类).files\image117.gif) 得
得(理工农医类).files\image119.gif)
故所求圆的方程为(x-1)2+(y-3)2=10.
(3)设P(x1,y1),Q(x2,y2)为抛物线上关于直线OB对称的两点,则
(理工农医类).files\image121.gif) 得
得(理工农医类).files\image123.gif)
即x1、x2为方程(理工农医类).files\image125.gif) 的两个相异实根,
的两个相异实根,
于是由(理工农医类).files\image127.gif) 得
得(理工农医类).files\image129.gif)
故当(理工农医类).files\image131.gif) 时,抛物线y =ax2-1上总有关于直线OB对称的两点.
时,抛物线y =ax2-1上总有关于直线OB对称的两点.
(22)[解](1)对于非零常数T,f (x+T)=x+T,Tf (x)=Tx.
因为对任意x∈R,x+T =Tx不能恒成立,
(理工农医类).files\image132.gif) 所以f (x)=x M .
所以f (x)=x M .
(2)因为函数f (x)=ax (a>0且a≠1)的图象与函数y=x的图象有公共点,
所以方程组:(理工农医类).files\image134.gif) 有解,消去y得ax=x,
有解,消去y得ax=x,
显然x=0不是方程的ax=x解,所以存在非零常数T,使aT=T.
于是对于f (x)=ax ,有
f (x+T)=ax+T = aT?ax=T?ax =T f (x),
故f (x)=ax∈M.
(3)当k=0时,f (x)=0,显然f (x)=0∈M.
当k≠0时,因为f (x)=sinkx∈M,所以存在非零常数T,
对任意x∈R,有
f (x+T)= T f (x)成立,即sin(kx+kT)= T sinkx.
因为k≠0时,且x∈R,所以kx∈R,kx+kT∈R,
于是sinkx∈[-1,1],sin(kx+kT) ∈[-1,1],
故要使sin(kx+kT) = Tsinkx成立,只有T=±1.
当T=1时,sin(kx+k)= sinkx成立,则k=2mp,m∈Z.
当T=-1时,sin(kx-k)= -sinkx成立,
即sin(kx-k+p) = sinkx成立,
则-k+p =2mp,m∈Z,即k= -(2m-1) p,m∈Z.
综合得,实数k的取值范围是{k | k= mp,m∈Z }.
 ,点B在直线
,点B在直线 上运动,当线段AB最短时,点B的极坐标为__________。
上运动,当线段AB最短时,点B的极坐标为__________。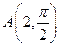 ,点B在直线
,点B在直线 上运动,当线段AB最短时,点B的极坐标为__________。
上运动,当线段AB最短时,点B的极坐标为__________。 点B在直线
点B在直线 上运动,则点A和点B间的最短距离为____________.
上运动,则点A和点B间的最短距离为____________. 点B在直线
点B在直线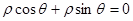 上运动,则点A和点B间的最短距离为____________.
上运动,则点A和点B间的最短距离为____________.