摘要:?n=3x+y=0.
网址:http://m.1010jiajiao.com/timu_id_20350[举报]
(2012•潍坊二模)①函数y=sin(x-
)在[0,π]上是减函数;
②点A(1,1)、B(2,7)在直线3x-y=0两侧;
③数列{an}为递减的等差数列,a1+a5=0,设数列{an}的前n项和为Sn,则当n=4时,Sn取得最大值;
④定义运算
=a1b2-a2b1则函数f(x)=
的图象在点(1,
)处的切线方程是6x-3y-5=0.
其中正确命题的序号是
查看习题详情和答案>>
| π |
| 2 |
②点A(1,1)、B(2,7)在直线3x-y=0两侧;
③数列{an}为递减的等差数列,a1+a5=0,设数列{an}的前n项和为Sn,则当n=4时,Sn取得最大值;
④定义运算
|
|
|
|
| 1 |
| 3 |
其中正确命题的序号是
②④
②④
(把所有正确命题的序号都写上).(2010•广东模拟)已知数列{an}的首项为a1=3,点(an,an+1)在直线3x-y=0(n∈N*)上.
(1)求数列{an}的通项公式;
(2)若f(x)=a1x+a2x2+…+anxn,求f'(1)的值,并化简.
查看习题详情和答案>>
(1)求数列{an}的通项公式;
(2)若f(x)=a1x+a2x2+…+anxn,求f'(1)的值,并化简.
(2010•广东模拟)已知数列{an}的首项为a1=3,点(an,an+1)在直线3x-y=0(n∈N*)上.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若f(x)=a1x+a2x2+…+anxn,求f'(1)的值,并化简.
(Ⅲ)若cn=log3an3-2(n∈N*),证明对任意的n∈N*,不等式(1+
)(1+
)•…•(1+
)>
恒成立.
查看习题详情和答案>>
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若f(x)=a1x+a2x2+…+anxn,求f'(1)的值,并化简.
(Ⅲ)若cn=log3an3-2(n∈N*),证明对任意的n∈N*,不等式(1+
| 1 |
| c1 |
| 1 |
| c2 |
| 1 |
| cn |
| 3 | 3n+1 |
 在[0,π]上是减函数;
在[0,π]上是减函数;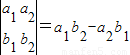 则函数
则函数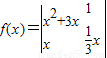 的图象在点
的图象在点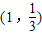 处的切线方程是6x-3y-5=0.
处的切线方程是6x-3y-5=0.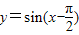 在[0,π]上是减函数;
在[0,π]上是减函数; 则函数
则函数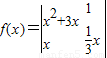 的图象在点
的图象在点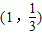 处的切线方程是6x-3y-5=0.
处的切线方程是6x-3y-5=0.