题目内容
①函数 在[0,π]上是减函数;
在[0,π]上是减函数;②点A(1,1)、B(2,7)在直线3x-y=0两侧;
③数列{an}为递减的等差数列,a1+a5=0,设数列{an}的前n项和为Sn,则当n=4时,Sn取得最大值;
④定义运算
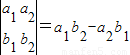 则函数
则函数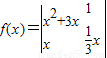 的图象在点
的图象在点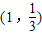 处的切线方程是6x-3y-5=0.
处的切线方程是6x-3y-5=0.其中正确命题的序号是 (把所有正确命题的序号都写上).
【答案】分析:①,利用诱导公式将y=sin(x-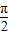 )转化为y=-cosx,利用余弦函数的单调性即可判断其正误;
)转化为y=-cosx,利用余弦函数的单调性即可判断其正误;
②,将A(1,1)、B(2,7)的坐标分别代入3x-y,观察乘积的符号即可判断;
③,由题意结合等差数列的性质可判断③的正误;
④,依题意可求得f(x)的解析式,从而可求得在点(1, )处的切线方程,继而可作出判断;
)处的切线方程,继而可作出判断;
解答:解:①,∵y=sin(x-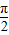 )=-cosx,在[0,π]上是增函数,故①错误;
)=-cosx,在[0,π]上是增函数,故①错误;
②,将A(1,1)、B(2,7)的坐标分别代入3x-y得(3×1-1)•(3×2-7)=-2<0,故点A(1,1)、B(2,7)在直线3x-y=0两侧,即②正确;
③,∵数列{an}为递减的等差数列,a1+a5=0,又a1+a5=2a3,
∴2a3=0,
故当n=2或3时Sn取得最大值,故③错误;
④,∵ =a1b2-a2b1,
=a1b2-a2b1,
∴f(x)=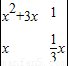 =
= x3+x2-x,
x3+x2-x,
∴[f′(x)]|x=1=(x2+2x-1)|x=1=2,
∴f(x)的图象在点(1, )处的切线方程为:y-
)处的切线方程为:y- =2(x-1),整理得:6x-3y-5=0,故④正确;
=2(x-1),整理得:6x-3y-5=0,故④正确;
综上所述,正确答案为②④.
故答案为:②④.
点评:本题考查命题的真假判断与应用,考查三角函数、平面区域、等差数列、及函数与导数等知识,属于中档题.
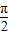 )转化为y=-cosx,利用余弦函数的单调性即可判断其正误;
)转化为y=-cosx,利用余弦函数的单调性即可判断其正误;②,将A(1,1)、B(2,7)的坐标分别代入3x-y,观察乘积的符号即可判断;
③,由题意结合等差数列的性质可判断③的正误;
④,依题意可求得f(x)的解析式,从而可求得在点(1,
 )处的切线方程,继而可作出判断;
)处的切线方程,继而可作出判断;解答:解:①,∵y=sin(x-
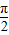 )=-cosx,在[0,π]上是增函数,故①错误;
)=-cosx,在[0,π]上是增函数,故①错误;②,将A(1,1)、B(2,7)的坐标分别代入3x-y得(3×1-1)•(3×2-7)=-2<0,故点A(1,1)、B(2,7)在直线3x-y=0两侧,即②正确;
③,∵数列{an}为递减的等差数列,a1+a5=0,又a1+a5=2a3,
∴2a3=0,
故当n=2或3时Sn取得最大值,故③错误;
④,∵
 =a1b2-a2b1,
=a1b2-a2b1,∴f(x)=
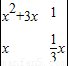 =
= x3+x2-x,
x3+x2-x,∴[f′(x)]|x=1=(x2+2x-1)|x=1=2,
∴f(x)的图象在点(1,
 )处的切线方程为:y-
)处的切线方程为:y- =2(x-1),整理得:6x-3y-5=0,故④正确;
=2(x-1),整理得:6x-3y-5=0,故④正确;综上所述,正确答案为②④.
故答案为:②④.
点评:本题考查命题的真假判断与应用,考查三角函数、平面区域、等差数列、及函数与导数等知识,属于中档题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
