摘要:(2)已知函数..试比较与的大小.解:(1)根据同底数幂的运算法则.可考虑用比值比较法.
网址:http://m.1010jiajiao.com/timu_id_198626[举报]
已知函数f(x)=2x+a.
(1)对于任意的实数x1,x2,试比较
与f(
-1)的大小;
(2)已知P=[1,4],关于x的不等式f(ax2-4x)>4+a的解集为M,且P∩M≠?,求实数a的取值范围. 查看习题详情和答案>>
(1)对于任意的实数x1,x2,试比较
| f(x1-1)+f(x2-1) |
| 2 |
| x1+x2 |
| 2 |
(2)已知P=[1,4],关于x的不等式f(ax2-4x)>4+a的解集为M,且P∩M≠?,求实数a的取值范围. 查看习题详情和答案>>
已知函数f(x)=
x+
,h(x)=
.
(Ⅰ)设函数F(x)=f(x)-h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程㏒4[
f(x-1)-
]=log2h(a-x)-log2h(4-x);
(Ⅲ)试比较f(100)h(100)-
h(k)与
的大小.
查看习题详情和答案>>
| 2 |
| 3 |
| 1 |
| 2 |
| x |
(Ⅰ)设函数F(x)=f(x)-h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程㏒4[
| 3 |
| 2 |
| 3 |
| 4 |
(Ⅲ)试比较f(100)h(100)-
| 100 |
 |
| k=1 |
| 1 |
| 6 |
已知函数f(x)=2x+a.
(1)对于任意的实数x1,x2,试比较
与f(
-1)的大小;
(2)已知P=[1,4],关于x的不等式f(ax2-4x)>4+a的解集为M,且P∩M≠?,求实数a的取值范围.
查看习题详情和答案>>
(1)对于任意的实数x1,x2,试比较
| f(x1-1)+f(x2-1) |
| 2 |
| x1+x2 |
| 2 |
(2)已知P=[1,4],关于x的不等式f(ax2-4x)>4+a的解集为M,且P∩M≠?,求实数a的取值范围.
 x+
x+ ,h(x)=
,h(x)=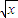 .
. f(x-1)-
f(x-1)- ]=㏒2h(a-x)-㏒2h(4-x);
]=㏒2h(a-x)-㏒2h(4-x); 与
与 的大小.
的大小.