摘要:解:过A1作A1D⊥AB于D.由于OD是A1D在平面ABC内的射影.AB⊥OD,D是AB的中点.这样A1A=,AD=1=A1D,=2×1=2.同理=2.S底=×2×=.
网址:http://m.1010jiajiao.com/timu_id_196260[举报]
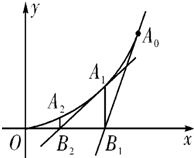 顶点在坐标原点,开口向上的抛物线经过A0(1,1),过A0作抛物 线的切线交x轴于B1,过B1点作x轴的垂线交抛物线于A1,过A1作抛物线的切线交x轴于B2,…,过An(xn,yn)作抛物线的切线交x轴于Bn+1(xn+1,0)
顶点在坐标原点,开口向上的抛物线经过A0(1,1),过A0作抛物 线的切线交x轴于B1,过B1点作x轴的垂线交抛物线于A1,过A1作抛物线的切线交x轴于B2,…,过An(xn,yn)作抛物线的切线交x轴于Bn+1(xn+1,0)(1)求{xn},{yn}的通项公式;
(2)设an=
| 1 |
| 1+xn |
| 1 |
| 1-xn+1 |
| 1 |
| 2 |
(3)设bn=1-log2yn,若对任意正整数n,不等式(1+
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 2n+3 |
已知抛物线C:y=x2,从原点O出发且斜率为k0的直线l0交抛物线C于一异于O点的点A1(x1,y1),过A1作一斜率为k1的直线l1交抛物线C于一异于A1的点A2(x2,y2)…,过An作斜率为kn的直线ln交抛物线C于一异于An的点An+1(xn+1,yn+1)且知kn=k0n+1(k0>0且k0≠1).
(1)求x1,x2以及xn与xn+1之间的递推关系式;
(2)求{xn}的通项公式.
查看习题详情和答案>>
(1)求x1,x2以及xn与xn+1之间的递推关系式;
(2)求{xn}的通项公式.
(2003•崇文区一模)正三棱台ABC-A1B1C1的上、下底面面积之比为1:4,过A1作平行于侧面B1BCC1的截面A1DE,D、E分别在AB、AC边上,则多面体A1-ADE与多面体A1B1C1-DBCE的体积之比为
查看习题详情和答案>>
1:6
1:6
.(2009•黄冈模拟)已知抛物线C:y2=2px的准线方程x=-
,C与直线?1:y=x在第一象限相交于点P1,过P1作C的切线m1,过P1作m1的垂线g1交x轴正半轴于点A1,过A1作?1的平行线?2交抛物线C于第一象限内的点P2,过P2作抛物线C1的切线m2,过P2作m2的垂线g2交x轴正半轴于点A2,…,依此类推,在x轴上形成一点列A1,A2,A3,…,An(n∈N*),设点An的坐标为(an,0).
(Ⅰ)试探求an+1关于an的递推关系式;
(Ⅱ)求证:an≤3•2n-1-
;
(Ⅲ)求证:
+
+…+
≥
-
.
查看习题详情和答案>>
| 1 |
| 4 |
(Ⅰ)试探求an+1关于an的递推关系式;
(Ⅱ)求证:an≤3•2n-1-
| 3 |
| 2 |
(Ⅲ)求证:
| 3 |
| (2a1+3)•2 |
| 4 |
| (2a2+3)•6 |
| n+2 |
| (2an+3)•n•(n+1) |
| 1 |
| 3 |
| 1 |
| 3•2n•(n+1) |
 如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.
如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.