摘要:复习:(1)对数的定义 .其中 a 与 N的取值范围,
网址:http://m.1010jiajiao.com/timu_id_194406[举报]
已知函数f(x)=
x3+
x2+(a2-3a)x-2a
(1)如果对任意x∈(1,2],f'(x)>a2恒成立,求实数a的取值范围;
(2)设实数f(x)的两个极值点分别为x1x2判断①x1+x2+a②x12+x22+a2③x13+x23+a3是否为定值?若是定值请求出;若不是定值,请把不是定值的表示为函数g(a)并求出g(a)的最小值;
(3)对于(2)中的g(a),设H(x)=
[g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.
查看习题详情和答案>>
| 1 |
| 3 |
| a-3 |
| 2 |
(1)如果对任意x∈(1,2],f'(x)>a2恒成立,求实数a的取值范围;
(2)设实数f(x)的两个极值点分别为x1x2判断①x1+x2+a②x12+x22+a2③x13+x23+a3是否为定值?若是定值请求出;若不是定值,请把不是定值的表示为函数g(a)并求出g(a)的最小值;
(3)对于(2)中的g(a),设H(x)=
| 1 |
| 9 |
(2013•青岛一模)若任意直线l过点F(0,1),且与函数f(x)=
x2的图象C于两个不同的点A,B过点A,BC,两切线交于点M
(Ⅰ)证明:点M纵坐标是一个定值,并求出这个定值;
(Ⅱ)若不等式f(x)≥g(x),g(x)=alnx(a>0),求实数a取值范围;
(Ⅲ)求证:
+
+
+…+
≤
,(其中e自然对数的底数,n≥2,n∈N).
查看习题详情和答案>>
| 1 |
| 4 |
(Ⅰ)证明:点M纵坐标是一个定值,并求出这个定值;
(Ⅱ)若不等式f(x)≥g(x),g(x)=alnx(a>0),求实数a取值范围;
(Ⅲ)求证:
| 2ln2 |
| 22 |
| 2ln3 |
| 32 |
| 2ln4 |
| 42 |
| 2ln |
| n2 |
| n-1 |
| e |
已知函数f(x)= x3+
x3+ x2+(a2-3a)x-2a
x2+(a2-3a)x-2a
(1)如果对任意x∈(1,2],f'(x)>a2恒成立,求实数a的取值范围;
(2)设实数f(x)的两个极值点分别为x1x2判断①x1+x2+a②x12+x22+a2③x13+x23+a3是否为定值?若是定值请求出;若不是定值,请把不是定值的表示为函数g(a)并求出g(a)的最小值;
(3)对于(2)中的g(a),设H(x)= [g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.
[g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.
查看习题详情和答案>>
 x3+
x3+ x2+(a2-3a)x-2a
x2+(a2-3a)x-2a(1)如果对任意x∈(1,2],f'(x)>a2恒成立,求实数a的取值范围;
(2)设实数f(x)的两个极值点分别为x1x2判断①x1+x2+a②x12+x22+a2③x13+x23+a3是否为定值?若是定值请求出;若不是定值,请把不是定值的表示为函数g(a)并求出g(a)的最小值;
(3)对于(2)中的g(a),设H(x)=
 [g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.
[g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.查看习题详情和答案>>
 x3+
x3+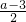 x2+(a2-3a)x-2a
x2+(a2-3a)x-2a [g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.
[g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.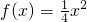 的图象C于两个不同的点A,B过点A,BC,两切线交于点M
的图象C于两个不同的点A,B过点A,BC,两切线交于点M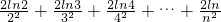
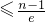 ,(其中e自然对数的底数,n≥2,n∈N).
,(其中e自然对数的底数,n≥2,n∈N).