题目内容
已知函数f(x)= x3+
x3+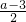 x2+(a2-3a)x-2a
x2+(a2-3a)x-2a
(1)如果对任意x∈(1,2],f'(x)>a2恒成立,求实数a的取值范围;
(2)设实数f(x)的两个极值点分别为x1x2判断①x1+x2+a②x12+x22+a2③x13+x23+a3是否为定值?若是定值请求出;若不是定值,请把不是定值的表示为函数g(a)并求出g(a)的最小值;
(3)对于(2)中的g(a),设H(x)= [g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.
[g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.
解:(1)∵函数f(x)= x3+
x3+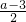 x2+(a2-3a)x-2a
x2+(a2-3a)x-2a
∴函数f′(x)=x2+(a-3)x+(a2-3a)
则f′(x)-a2=x2+(a-3)x-3a=(x+a)(x-3)
若对任意x∈(1,2],f'(x)>a2恒成立,
则对任意x∈(1,2],f′(x)-a2>0恒成立
则a<-2.
(2)令f′(x)=0
则x=3或x=-a
则①x1+x2+a=3为定值;
②x12+x22+a2=2a2+9不为定值;
此时g(a)=2a2+9,当a=0时有最小值9;
③x13+x23+a3=27为定值;
(3)∵g(a)=2a2+9,
∴H(x)= [g(x)-27]=
[g(x)-27]= (2x2-18),
(2x2-18),
令F(x)=H(x)-ex= (2x2-18)-ex,
(2x2-18)-ex,
则F′(x)= x-ex,
x-ex,
当x∈(0,1)时,F′(x)<0恒成立
即F(x)在区间(0,1)上为减函数
当m,n∈(0,1)且m≠n时,不妨令m>n
则F(m)-F(n)=[H(m)-em]-[H(n)-en]<0
即[H(m)-em]<[H(n)-en]
即H(m)-H(m)<em-en,
即|H(m)-H(n)|<|em-en|
分析:(1)由已知中函数f(x)= x3+
x3+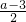 x2+(a2-3a)x-2a,可求出f'(x)的解析式,根据二次函数的图象和性质可得对任意x∈(1,2],f'(x)>a2恒成立时,实数a的取值范围;
x2+(a2-3a)x-2a,可求出f'(x)的解析式,根据二次函数的图象和性质可得对任意x∈(1,2],f'(x)>a2恒成立时,实数a的取值范围;
(2)由(1)中f'(x)的解析式,可求出x1x2,进而判断出①x1+x2+a②x12+x22+a2③x13+x23+a3是否为定值及函数g(a)的解析式,及g(a)的最小值;
(3)根据(2)中g(a)的解析式,我们可以求出H(x)= [g(x)-27]的解析式,构造函数F(x)=H(x)-ex,利用导数法,可判断出F(x)在区间(0,1)上的单调性,进而判断出当m,n∈(0,1)且m≠n时,|H(m)-H(n)|与|em-en|的大小.
[g(x)-27]的解析式,构造函数F(x)=H(x)-ex,利用导数法,可判断出F(x)在区间(0,1)上的单调性,进而判断出当m,n∈(0,1)且m≠n时,|H(m)-H(n)|与|em-en|的大小.
点评:本题考查的知识点是利用导数求闭区间上函数的最值,函数恒成立问题,导数的运算,其中(1)的关键是熟练掌握二次函数的图象和性质,(2)的关键是求出f(x)的两个极值点分别为x1x2,(3)的关键是构造函数F(x)=H(x)-ex,并利用导数法判断出F(x)在区间(0,1)上的单调性.
 x3+
x3+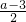 x2+(a2-3a)x-2a
x2+(a2-3a)x-2a∴函数f′(x)=x2+(a-3)x+(a2-3a)
则f′(x)-a2=x2+(a-3)x-3a=(x+a)(x-3)
若对任意x∈(1,2],f'(x)>a2恒成立,
则对任意x∈(1,2],f′(x)-a2>0恒成立
则a<-2.
(2)令f′(x)=0
则x=3或x=-a
则①x1+x2+a=3为定值;
②x12+x22+a2=2a2+9不为定值;
此时g(a)=2a2+9,当a=0时有最小值9;
③x13+x23+a3=27为定值;
(3)∵g(a)=2a2+9,
∴H(x)=
 [g(x)-27]=
[g(x)-27]= (2x2-18),
(2x2-18),令F(x)=H(x)-ex=
 (2x2-18)-ex,
(2x2-18)-ex,则F′(x)=
 x-ex,
x-ex,当x∈(0,1)时,F′(x)<0恒成立
即F(x)在区间(0,1)上为减函数
当m,n∈(0,1)且m≠n时,不妨令m>n
则F(m)-F(n)=[H(m)-em]-[H(n)-en]<0
即[H(m)-em]<[H(n)-en]
即H(m)-H(m)<em-en,
即|H(m)-H(n)|<|em-en|
分析:(1)由已知中函数f(x)=
 x3+
x3+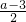 x2+(a2-3a)x-2a,可求出f'(x)的解析式,根据二次函数的图象和性质可得对任意x∈(1,2],f'(x)>a2恒成立时,实数a的取值范围;
x2+(a2-3a)x-2a,可求出f'(x)的解析式,根据二次函数的图象和性质可得对任意x∈(1,2],f'(x)>a2恒成立时,实数a的取值范围;(2)由(1)中f'(x)的解析式,可求出x1x2,进而判断出①x1+x2+a②x12+x22+a2③x13+x23+a3是否为定值及函数g(a)的解析式,及g(a)的最小值;
(3)根据(2)中g(a)的解析式,我们可以求出H(x)=
 [g(x)-27]的解析式,构造函数F(x)=H(x)-ex,利用导数法,可判断出F(x)在区间(0,1)上的单调性,进而判断出当m,n∈(0,1)且m≠n时,|H(m)-H(n)|与|em-en|的大小.
[g(x)-27]的解析式,构造函数F(x)=H(x)-ex,利用导数法,可判断出F(x)在区间(0,1)上的单调性,进而判断出当m,n∈(0,1)且m≠n时,|H(m)-H(n)|与|em-en|的大小.点评:本题考查的知识点是利用导数求闭区间上函数的最值,函数恒成立问题,导数的运算,其中(1)的关键是熟练掌握二次函数的图象和性质,(2)的关键是求出f(x)的两个极值点分别为x1x2,(3)的关键是构造函数F(x)=H(x)-ex,并利用导数法判断出F(x)在区间(0,1)上的单调性.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|