摘要:[总结]1.建立函数模型的一般方法图示为:实际问题一般的函数关系式;或:实际问题一般的函数关系式
网址:http://m.1010jiajiao.com/timu_id_194335[举报]
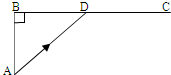 如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,先乘船,船速为25km/h,再乘汽车,车速为50km/h.设登陆点在D处,从A到C所用的时间为y(单位:h).
如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,先乘船,船速为25km/h,再乘汽车,车速为50km/h.设登陆点在D处,从A到C所用的时间为y(单位:h).(1)按下列要求建立函数关系:①设∠BAD=θ(rad),将y表示为θ的函数;②设BD=x(km),将y表示为x的函数.
(2)请选用(1)中的一个函数关系,确定登陆点D的位置,使从A到C所用时间最少?并求出所用的最少时间. 查看习题详情和答案>>
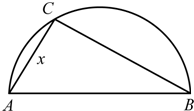 两县城A和B相距20km,现计划在两城外以AB为直径的半圆弧
两县城A和B相距20km,现计划在两城外以AB为直径的半圆弧 |
| AB |
 |
| AB |
(1)按下列要求建立函数关系式:
①设∠CAB=θ(rad),将θ表示成y 的函数;并写出函数的定义域.
②设AC=x(km),将x表示成y的函数;并写出函数的定义域.
(2)请你选用(1)中的一个函数关系确定垃圾处理厂的位置,使建在此处的垃圾处理厂对城A和城B的总影响度最小?
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数y=f(x)模型制定奖励方案,试用数学语言表述该公司对奖励函数f(x)模型的基本要求,并分析函数y=
+2是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用模型函数y=
作为奖励函数模型,试确定最小的正整数a的值.
查看习题详情和答案>>
(1)若建立函数y=f(x)模型制定奖励方案,试用数学语言表述该公司对奖励函数f(x)模型的基本要求,并分析函数y=
| x |
| 150 |
(2)若该公司采用模型函数y=
| 10x-3a |
| x+2 |
 (2011•奉贤区二模)用2π平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为x,圆锥母线的长为y
(2011•奉贤区二模)用2π平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为x,圆锥母线的长为y