题目内容
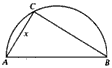
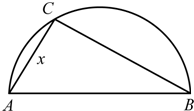 两县城A和B相距20km,现计划在两城外以AB为直径的半圆弧
两县城A和B相距20km,现计划在两城外以AB为直径的半圆弧 |
| AB |
 |
| AB |
(1)按下列要求建立函数关系式:
①设∠CAB=θ(rad),将θ表示成y 的函数;并写出函数的定义域.
②设AC=x(km),将x表示成y的函数;并写出函数的定义域.
(2)请你选用(1)中的一个函数关系确定垃圾处理厂的位置,使建在此处的垃圾处理厂对城A和城B的总影响度最小?
分析:(1)①设∠CAB=θ(rad),AC=20cosθ,BC=20sinθ,结合当垃圾处理厂建在
的中点时,对城A和城B的总影响度为0.065,则可得函数解析式,并可写出函数的定义域;
②先利用AC⊥BC,求出,再利用圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,得到y和x之间的函数关系,最后利用垃圾处理厂建在的中点时,对城A和城B的总影响度为0.065求出k即可求出结果.
(2)先求出导函数以及导数为0的根,进而求出其单调区间,找到函数的最小值即可.
 |
| AB |
②先利用AC⊥BC,求出,再利用圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,得到y和x之间的函数关系,最后利用垃圾处理厂建在的中点时,对城A和城B的总影响度为0.065求出k即可求出结果.
(2)先求出导函数以及导数为0的根,进而求出其单调区间,找到函数的最小值即可.
解答:解:(1)①在直角△ABC中,AC=20cosθ,BC=20sinθ,则y=
+
(0<θ<
)
当x=10
时,y=0.065,所以k=9
所以y表示成x的函数为y=
+
(0<θ<
);
②由题意知AC⊥BC,BC2=400-x2,y=
+
(0<x<20)
(2)选②,则y′=
,
令y'=0得18x4=8(400-x2)2,
所以x2=160,即x=4
,
当0<x<4
时,18x4<8(400-x2)2,即y'<0,以函数为单调减函数,
当4
<x<20时,18x4>8(400-x2)2,即y'>0,所以函数为单调增函数.
所以当x=4
时,即当C点到城A的距离为4
时,函数y=
+
(0<x<20)有最小值.
| 4 |
| 400cos2θ |
| k |
| 400sin2θ |
| π |
| 2 |
当x=10
| 2 |
所以y表示成x的函数为y=
| 4 |
| 400cos2θ |
| 9 |
| 400sin2θ |
| π |
| 2 |
②由题意知AC⊥BC,BC2=400-x2,y=
| 4 |
| x2 |
| 9 |
| 400-x2 |
(2)选②,则y′=
| 18x4-8(400-x2)2 |
| x3(400-x2)2 |
令y'=0得18x4=8(400-x2)2,
所以x2=160,即x=4
| 10 |
当0<x<4
| 10 |
当4
| 10 |
所以当x=4
| 10 |
| 10 |
| 4 |
| x2 |
| 9 |
| 400-x2 |
点评:本题主要考查函数在实际生活中的应用问题,涉及到函数解析式的求法以及利用导数研究函数的最值问题,属于中档题目

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
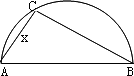
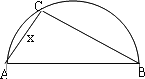
 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在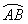 的中点时,对城A和城B的总影响度为0.065,
的中点时,对城A和城B的总影响度为0.065,