摘要：解:原不等式即a<-()x-()x恒成立.设-()x-()x=f(x),只要a<fmin↓.fmin=-1,∴a<-1[补充习题]
网址：http://m.1010jiajiao.com/timu_id_194271[举报]
解关于
的不等式
【解析】本试题主要考查了含有参数的二次不等式的求解，
首先对于二次项系数a的情况分为三种情况来讨论，
A=0,a>0,a<0,然后结合二次函数的根的情况和图像与x轴的位置关系，得到不等式的解集。
解：①若a=0，则原不等式变为-2x+2<0即x>1
此时原不等式解集为
； 
②若a>0，则ⅰ）
时，原不等式的解集为
；
ⅱ）
时，原不等式的解集为
；
ⅲ）
时，原不等式的解集为
。 
③若a<0，则原不等式变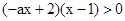为
原不等式的解集为
。
查看习题详情和答案>>
研究问题：“已知关于x的不等式ax2-bx+c＞0，解集为（1，2），解关于x的不等式cx2-bx+a＞0”有如下解法：
解：由cx2-bx+a＞0且x≠0，所以
＞0得a（
）2-
+c＞0，设
=y，得ay2-by+c＞0，由已知得：1＜y＜2，即1＜
＜2，∴
＜x＜1所以不等式cx2-bx+a＞0的解集是（
，1）．
参考上述解法，解决如下问题：已知关于x的不等式
+
＜0的解集是：（-3，-1）∪（2，4），则不等式
+
＜0的解集是
查看习题详情和答案>>
解：由cx2-bx+a＞0且x≠0，所以
| (c×2-bx+a) |
| x2 |
| 1 |
| x |
| b |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
参考上述解法，解决如下问题：已知关于x的不等式
| b |
| (x+a) |
| (x+c) |
| (x+d) |
| bx |
| (ax-1) |
| (cx-1) |
| (dx-1) |
(-
，-
)∪(
，1)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
(-
，-
)∪(
，1)
．| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
（2012•吉安县模拟）选做题：请考生在下列两题中任选一题作答．若两题都做，则按做的第一题评阅计分．本题共5分．
（1）．（不等式选讲）若不等式||x-a|-2|＜1的解集是（-2，0）∪（2，4），则实数a=
（2）．（坐标系与参数方程）在极坐标系中，点M（4，
）到直线l：ρ（2cosθ+sinθ）=4的距离d=
．
查看习题详情和答案>>
（1）．（不等式选讲）若不等式||x-a|-2|＜1的解集是（-2，0）∪（2，4），则实数a=
1
1
（2）．（坐标系与参数方程）在极坐标系中，点M（4，
| π |
| 3 |
2
| ||
| 5 |
2
| ||
| 5 |