(2) 或时, [注:]按以下做法不扣分(以下是高考命题人给的原解)这种解法不太严谨,但也被大部分人所接受——青夏教育精英家教网——

摘要：(2) 或时, [注:]按以下做法不扣分(以下是高考命题人给的原解)这种解法不太严谨,但也被大部分人所接受

网址：http://m.1010jiajiao.com/timu_id_193493[举报]

设椭圆（常数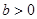）的左右焦点分别为，是直线上的两个动点，．

（1）若，求的值；

（2）求的最小值．

【解析】第一问中解：设，则

由得由，得

②

第二问易求椭圆的标准方程为：

，

所以，当且仅当或时，取最小值．

解：设， ……………………1分

则，由得 ①……2分

（1）由，得 ② ……………1分

③ ………………………1分

由①、②、③三式，消去，并求得． ………………………3分

（2）解法一：易求椭圆的标准方程为：．………………2分

， ……4分

所以，当且仅当或时，取最小值．…2分

解法二：， ………………4分

所以，当且仅当或时，取最小值

查看习题详情和答案>>

已知函数f（x）为奇函数，x＞0时为增函数且f（2）=0，则{x|f（x-2）＞0}=（　　）

A、{x|0＜x＜2或x＞4}

B、{x|x＜0或x＞4}

C、{x|x＜0或x＞6}

D、{x|x＜-2或x＞2}

查看习题详情和答案>>

粒子A位于数轴x=0处，粒子B位于x=2处，这两粒子每隔1秒向左或向右移动一个单位，设向右移动的概率为

，向左移的概率为

（1）求第三秒时，粒子A在点x=1处的概率
（2）求第2秒时，粒子A，B同在点x=2处的概率查看习题详情和答案>>

已知二次函数f（x）=ax²+bx+c（a≠0）且满足f（-1）=0对任意实数x，都有f（x）-x≥0，并且当x∈（0，2）时，有f(x)≤(

)2
（1）求f（1）的值；
（2）证明：a＞0、c＞0；
（3）当x∈[-1，1]时，g（x）=f（x）-mx（m∈R）是单调的，求证：m≤0或m≥1．查看习题详情和答案>>

已知二次函数f（x）=ax²+bx+c（a，b，c均为实数），满足a-b+c=0，对于任意实数x 都有f （x）-x≥0，并且当x∈（0，2）时，有f （x）≤(

)2．
（1）求f （1）的值；
（2）证明：ac≥

；
（3）当x∈[-2，2]且a+c取得最小值时，函数F（x）=f （x）-mx （m为实数）是单调的，求证：m≤-

．查看习题详情和答案>>