网址:http://m.1010jiajiao.com/timu_id_193337[举报]
已知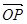 =
=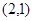 ,
,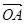 =
=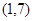 ,
, =
=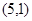 ,设
,设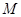 是直线
是直线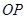 上一点,
上一点,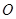 是坐标原点.
是坐标原点.
⑴求使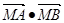 取最小值时的
取最小值时的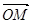 ;
⑵对(1)中的点
;
⑵对(1)中的点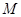 ,求
,求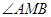 的余弦值.
的余弦值.
【解析】第一问中利用设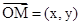 ,则根据已知条件,O,M,P三点共线,则可以得到x=2y,然后利用
,则根据已知条件,O,M,P三点共线,则可以得到x=2y,然后利用
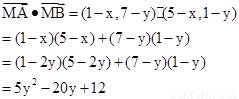
可知当x=4,y=2时取得最小值。
第二问中利用数量积的性质可以表示夹角的余弦值,进而得到结论。
(1)、因为设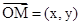 则
则
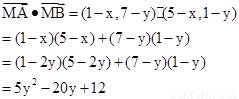
可知当x=4,y=2时取得最小值。此时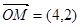 。
。
(2)
查看习题详情和答案>>
材料:为了美化环境,某房地产公司打算在所管辖的一个居民小区内的一块半圆形空地上,划出一个内接矩形辟为绿地,且使矩形的一边落在半圆的直径上,而另外两个顶点在半圆的圆周上,已知半圆的半径为30米.为了使绿地的面积最大,该公司请了本公司的一位设计师,设计出了这个半圆内接矩形的长与宽的关系.该设计师的计算过程如下:
如下图,设CD=x,则OD=![]() ,矩形的面积设为S,则
,矩形的面积设为S,则
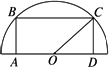
S=2x·![]() =
=![]() .
.
所以当x2=450,即x=![]() 时,S有最大值,即此时矩形的面积最大.
时,S有最大值,即此时矩形的面积最大.
问题:现在我们已经学习了三角函数的有关知识,利用三角函数的知识该如何解决这一问题?
设A是如下形式的2行3列的数表,
|
a |
b |
c |
|
d |
e |
f |
满足性质P:a,b,c,d,e,f ,且a+b+c+d+e+f=0
,且a+b+c+d+e+f=0
记 为A的第i行各数之和(i=1,2),
为A的第i行各数之和(i=1,2),  为A的第j列各数之和(j=1,2,3)记
为A的第j列各数之和(j=1,2,3)记 为
为 中的最小值。
中的最小值。
(1)对如下表A,求 的值
的值
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A形如
|
1 |
1 |
-1-2d |
|
d |
d |
-1 |
其中 ,求
,求 的最大值
的最大值
(3)对所有满足性质P的2行3列的数表A,求 的最大值。
的最大值。
【解析】(1)因为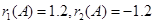 ,
, ,所以
,所以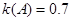
(2)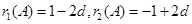 ,
,
因为 ,所以
,所以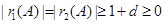 ,
,
所以
当d=0时, 取得最大值1
取得最大值1
(3)任给满足性质P的数表A(如图所示)
|
a |
b |
c |
|
d |
e |
f |
任意改变A的行次序或列次序,或把A中的每个数换成它的相反数,所得数表 仍满足性质P,并且
仍满足性质P,并且 ,因此,不妨设
,因此,不妨设 ,
, ,
,
由 得定义知,
得定义知, ,
, ,
, ,
,
从而

所以, ,由(2)知,存在满足性质P的数表A使
,由(2)知,存在满足性质P的数表A使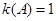 ,故
,故 的最大值为1
的最大值为1
【考点定位】此题作为压轴题难度较大,考查学生分析问题解决问题的能力,考查学生严谨的逻辑思维能力
查看习题详情和答案>>
 如图,已知△ABC中,∠C=
如图,已知△ABC中,∠C=| π |
| 2 |
(1)用a,θ表示△ABC的面积S和正方形DEFG的面积T;
(2)设f(θ)=
| T |
| S |
(3)通过对此题的解答,我们是否可以作如下推断:若需要从一块直角三角形的材料上裁剪一整块正方形(不得拼接),则这块材料的最大利用率要视该直角三角形的具体形状而定,但最大利用率不会超过第(2)小题中的结论P.请分析此推断是否正确,并说明理由.
已知函数f(x)=ex-ax,其中a>0.
(1)若对一切x∈R,f(x)  1恒成立,求a的取值集合;
1恒成立,求a的取值集合;
(2)在函数f(x)的图像上去定点A(x1, f(x1)),B(x2, f(x2))(x1<x2),记直线AB的斜率为k,证明:存在x0∈(x1,x2),使 恒成立.
恒成立.
【解析】解: 令
令 .
.
当 时
时 单调递减;当
单调递减;当 时
时 单调递增,故当
单调递增,故当 时,
时, 取最小值
取最小值
于是对一切 恒成立,当且仅当
恒成立,当且仅当 . ①
. ①
令 则
则
当 时,
时, 单调递增;当
单调递增;当 时,
时, 单调递减.
单调递减.
故当 时,
时, 取最大值
取最大值 .因此,当且仅当
.因此,当且仅当 时,①式成立.
时,①式成立.
综上所述, 的取值集合为
的取值集合为 .
.
(Ⅱ)由题意知, 令
令 则
则


令 ,则
,则 .当
.当 时,
时, 单调递减;当
单调递减;当 时,
时, 单调递增.故当
单调递增.故当 ,
, 即
即
从而 ,
, 又
又

所以
 因为函数
因为函数 在区间
在区间 上的图像是连续不断的一条曲线,所以存在
上的图像是连续不断的一条曲线,所以存在 使
使 即
即 成立.
成立.
【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等,考查运算能力,考查分类讨论思想、函数与方程思想等数学方法.第一问利用导函数法求出 取最小值
取最小值 对一切x∈R,f(x)
对一切x∈R,f(x)  1恒成立转化为
1恒成立转化为 从而得出求a的取值集合;第二问在假设存在的情况下进行推理,然后把问题归结为一个方程是否存在解的问题,通过构造函数,研究这个函数的性质进行分析判断.
从而得出求a的取值集合;第二问在假设存在的情况下进行推理,然后把问题归结为一个方程是否存在解的问题,通过构造函数,研究这个函数的性质进行分析判断.
查看习题详情和答案>>