题目内容
 如图,已知△ABC中,∠C=
如图,已知△ABC中,∠C=| π |
| 2 |
(1)用a,θ表示△ABC的面积S和正方形DEFG的面积T;
(2)设f(θ)=
| T |
| S |
(3)通过对此题的解答,我们是否可以作如下推断:若需要从一块直角三角形的材料上裁剪一整块正方形(不得拼接),则这块材料的最大利用率要视该直角三角形的具体形状而定,但最大利用率不会超过第(2)小题中的结论P.请分析此推断是否正确,并说明理由.
分析:(1)由题意可得AC=a•tanθ,故S=
•a•a•tanθ=
tanθ,θ∈(0,
).设正方形DEFG边长为m,则CG=mcosθ,BG=
,由此求出BC和m,再由T=m2求得结果.
(2)化简f(θ)=
=
令u=
+
+1,sin2θ∈(0,1].故当sin2θ=1时,u取得最小值,即f(θ)取得最大值,此时,sin2θ=1,θ=
.△ABC为等腰直角三角形.
(3)此推断不正确,若以如图方法裁剪,S=
tanθ,求出m和T,代入f(θ)=
化简可得
,θ∈(0,
),当且仅当
=
,tanθ=1,即 θ=
时,u取得最小值1,f(θ) 的最大值为
.此时△ABC为等腰直角三角形,再由
>
,得出结论.
| 1 |
| 2 |
| a2 |
| 2 |
| π |
| 2 |
| m |
| sinθ |
(2)化简f(θ)=
| T |
| S |
|
| sin2θ |
| 4 |
| 1 |
| sin2θ |
| π |
| 4 |
(3)此推断不正确,若以如图方法裁剪,S=
| a2 |
| 2 |
| T |
| S |
|
| π |
| 2 |
| tanθ |
| 2 |
| 1 |
| 2tanθ |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 9 |
解答: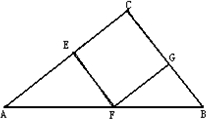 (1)解:∵在△ABC中,∴∠CBA=θ,BC=a.
(1)解:∵在△ABC中,∴∠CBA=θ,BC=a.
∴AC=a•tanθ.
∴S=
•a•a•tanθ=
tanθ,θ∈(0,
).
设正方形DEFG边长为m,则CG=mcosθ,BG=
,
∴BC=mcosθ+
=a.
∴m=
,
∴T=m2=
,θ∈(0,
).…(6分)
(2)解:由(1)可得
=
=
=
令u=
+
+1,sin2θ∈(0,1].
∴当sin2θ=1时,u取得最小值,即f(θ)取得最大值.
∴f(θ)=
的最大值为
.此时 sin2θ=1,θ=
.∴△ABC为等腰直角三角形.…(12分)
(3)解:此推断不正确,若以如图方法裁剪,S=
tanθ.
设正方形边长为m,∵
=tanθ,∴m=
,∴T=m2=(
)2.
∴f(θ)=
=
•
=
令 u=
+
,tanθ∈(0,+∞),
当且仅当
=
,tanθ=1,即 θ=
时,u取得最小值1.∴f(θ) 的最大值为
.
此时△ABC为等腰直角三角形.∵
>
,
∴材料的最大利用率超过了
,∴该推断并不正确. …(16分)
 (1)解:∵在△ABC中,∴∠CBA=θ,BC=a.
(1)解:∵在△ABC中,∴∠CBA=θ,BC=a.∴AC=a•tanθ.
∴S=
| 1 |
| 2 |
| a2 |
| 2 |
| π |
| 2 |
设正方形DEFG边长为m,则CG=mcosθ,BG=
| m |
| sinθ |
∴BC=mcosθ+
| m |
| sinθ |
∴m=
| asinθ |
| 1+sinθ•cosθ |
∴T=m2=
| a2sin2θ |
| (1+sinθ•cosθ)2 |
| π |
| 2 |
(2)解:由(1)可得
|
| 2sinθcosθ |
| (1+sinθcosθ)2 |
=
|
|
令u=
| sin2θ |
| 4 |
| 1 |
| sin2θ |
∴当sin2θ=1时,u取得最小值,即f(θ)取得最大值.
∴f(θ)=
| T |
| S |
| 4 |
| 9 |
| π |
| 4 |
(3)解:此推断不正确,若以如图方法裁剪,S=
| a2 |
| 2 |
设正方形边长为m,∵
| m |
| a-m |
| atanθ |
| tanθ+1 |
| atanθ |
| tanθ+1 |
∴f(θ)=
| T |
| S |
| a2•tan2θ |
| tan2θ+2tanθ+1 |
| 2 |
| a2•tanθ |
|
令 u=
| tanθ |
| 2 |
| 1 |
| 2tanθ |
当且仅当
| tanθ |
| 2 |
| 1 |
| 2tanθ |
| π |
| 4 |
| 1 |
| 2 |
此时△ABC为等腰直角三角形.∵
| 1 |
| 2 |
| 4 |
| 9 |
∴材料的最大利用率超过了
| 4 |
| 9 |
点评:本题主要考查在实际问题中运用三角函数模型,解三角形,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
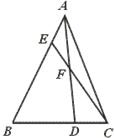 如图,已知△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于F.求
如图,已知△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于F.求 
 如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,
如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上, (2012•石家庄一模)如图,已知△ABC中,AB=
(2012•石家庄一模)如图,已知△ABC中,AB=