摘要:即有对任意恒成立.即
网址:http://m.1010jiajiao.com/timu_id_193105[举报]
在数列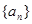 中,
中,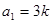 ,其中
,其中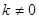 ,对任意
,对任意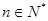 都有:
都有: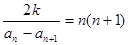 ;(1)求数列
;(1)求数列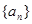 的第2项和第3项;
的第2项和第3项;
(2)求数列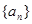 的通项公式
的通项公式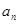 ,假设
,假设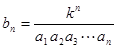 ,试求数列
,试求数列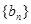 的前
的前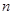 项和
项和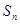 ;
;
(3)若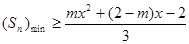 对一切
对一切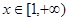 恒成立,求
恒成立,求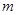 的取值范围。
的取值范围。
【解析】第一问中利用)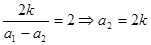 同理得到
同理得到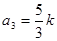
第二问中,由题意得到: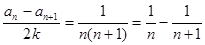
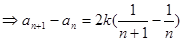
累加法得到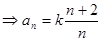
第三问中,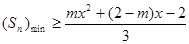 利用恒成立,转化为最小值大于等于即可。得到范围。
利用恒成立,转化为最小值大于等于即可。得到范围。
(1)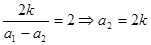 同理得到
同理得到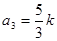 ……2分
……2分
(2)由题意得到: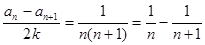
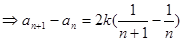
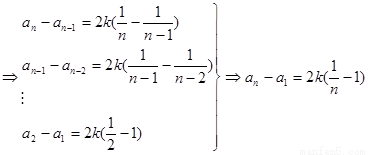 又
又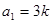
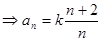 ……5分
……5分
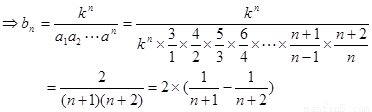
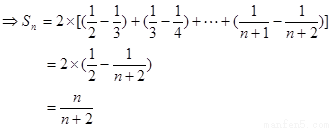 ……8分
……8分
(3)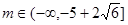
查看习题详情和答案>>
函数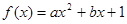 (
(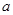 、
、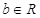 )满足:
)满足: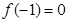 ,且对任意实数x均有
,且对任意实数x均有
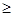 0成立
0成立
(1)求实数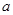 、
、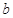 的值;
的值;
(2)当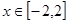 时,求函数
时,求函数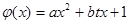 的最大值
的最大值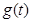 .
.
【解析】(1) 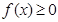 恒成立
恒成立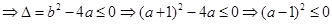 .
.
(2) 
对称轴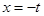 ,由于开口方向向上,所以求最大值时对称轴要与区间中间进行比较讨论即可.
,由于开口方向向上,所以求最大值时对称轴要与区间中间进行比较讨论即可.
查看习题详情和答案>>
设S是至少有两个元素的集合,在S上定义了一个二元运算“*”(即对任意的a,b∈S,对于有序实数对(a,b)在S中有唯一确定的元素a*b与之对应)若对任意的a,b∈S,有(a*b)*a=b,则对任意的a,b∈S,下列等式中不恒成立的是
[ ]
A.
(a*b)*a=a
B.
b*(b*b)=b
C.
[a*(b*a)]*(a*b)=a
D.
(a*b)*[b*(a*b)]=b