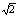设A是由m×n个实数组成的m行n列的数表，满足：每个数的绝对值不大于1，且所有数的和为零，记s(m，n)为所有这样的数表构成的集合。

对于A∈S(m,n),记r_i(A)为A的第ⅰ行各数之和（1≤ⅰ≤m），C_j(A)为A的第j列各数之和（1≤j≤n）：

记K(A)为∣r₁(A)∣,∣R₂(A)∣,…,∣Rm(A)∣,∣C₁(A)∣,∣C₂(A)∣,…,∣Cn(A)∣中的最小值。

（1）   对如下数表A，求K（A）的值；

（2）设数表A∈S（2,3）形如

求K（A）的最大值；

（3）给定正整数t，对于所有的A∈S（2,2t+1），求K（A）的最大值。

【解析】（1）因为，

所以

（2）  不妨设.由题意得.又因为，所以，

于是，，

所以，当，且时，取得最大值1。

（3）对于给定的正整数t，任给数表如下，

任意改变A的行次序或列次序，或把A中的每一个数换成它的相反数，所得数表

，并且，因此，不妨设，

且。

由得定义知，，

又因为

所以

所以，

对数表：

则且，

综上，对于所有的，的最大值为

仔细阅读下面问题的解法：

    设A=[0, 1],若不等式2^1-x-a＞0在A上有解,求实数a的取值范围。

    解：由已知可得  a ＜ 2^1-x

        令f(x)= 2^1-x ,∵不等式a ＜2^1-x在A上有解,

        ∴a ＜f(x)在A上的最大值.

        又f(x)在[0,1]上单调递减，f(x)_max =f(0)=2.  ∴实数a的取值范围为a＜2.

研究学习以上问题的解法，请解决下面的问题：

(1)已知函数f(x)=x²+2x+3(-2≤x≤-1)，求f(x)的反函数及反函数的定义域A；

(2)对于(1)中的A，设g(x)=，x∈A,试判断g(x)的单调性(写明理由，不必证明)；

(3)若B ={x|＞2^x+a–5}，且对于(1)中的A，A∩B≠F，求实数a的取值范围。

如图，四棱锥S—ABCD中，SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点，SE=2EB

(Ⅰ)证明：平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小                .

【解析】本试题主要考查了立体几何中的运用。

(1)证明：因为SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点，SE=2EB   所以ED⊥BS,DE⊥EC,所以ED⊥平面SBC.，因此可知得到平面EDC⊥平面SBC.

（Ⅱ）由SA²= SD²+AD² = 5 ，AB=1，SE=2EB，AB⊥SA，知

AE²= (1 /3 SA)²+(2/ 3 AB)² =1，又AD=1．

故△ADE为等腰三角形．

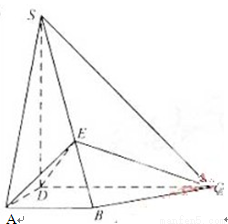
取ED中点F，连接AF，则AF⊥DE，AF²= AD²-DF² =．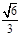

连接FG，则FG∥EC，FG⊥DE．

所以，∠AFG是二面角A-DE-C的平面角．

连接AG，AG= 2 ，FG²= DG²-DF² =，

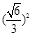cos∠AFG=(AF²+FG²-AG² )/2⋅AF⋅FG =-1 /2 ，

所以，二面角A-DE-C的大小为120°