题目内容
仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围。
解:由已知可得 a<21-x
令f(x)=21-x,∵不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值.
又f(x)在[0,1]上单调递减,f(x)max ="f(0)=2. " ∴实数a的取值范围为a<2.
研究学习以上问题的解法,请解决下面的问题:
(1)已知函数f(x)=x2+2x+3(-2≤x≤-1),求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)= ,x∈A,试判断g(x)的单调性(写明理由,不必证明);
,x∈A,试判断g(x)的单调性(写明理由,不必证明);
(3)若B={x| >2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。
>2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围。
解:由已知可得 a<21-x
令f(x)=21-x,∵不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值.
又f(x)在[0,1]上单调递减,f(x)max ="f(0)=2. " ∴实数a的取值范围为a<2.
研究学习以上问题的解法,请解决下面的问题:
(1)已知函数f(x)=x2+2x+3(-2≤x≤-1),求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)=
 ,x∈A,试判断g(x)的单调性(写明理由,不必证明);
,x∈A,试判断g(x)的单调性(写明理由,不必证明);(3)若B={x|
 >2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。
>2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。(1)f-1(x)=-1-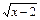 x∈[2,3] A=[2,3]
x∈[2,3] A=[2,3]
(2)g(x)在x∈[2,3]上单调递减(3)a的取值范围为(-∞,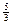 ) …
) …
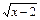 x∈[2,3] A=[2,3]
x∈[2,3] A=[2,3](2)g(x)在x∈[2,3]上单调递减(3)a的取值范围为(-∞,
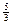 ) …
) … (1)f(x)=(x+1)2+2
∵f(x)在[-2,-1]上单调递减∴f(x)∈[2,3],故反函数的定义域A=[2,3]……2分
x+1=-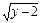 ,x=-1-
,x=-1-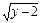 ∴f-1(x)=-1-
∴f-1(x)=-1-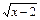 x∈[2,3] …………4分
x∈[2,3] …………4分

∵f(x)在[-2,-1]上单调递减∴f(x)∈[2,3],故反函数的定义域A=[2,3]……2分
x+1=-
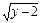 ,x=-1-
,x=-1-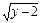 ∴f-1(x)=-1-
∴f-1(x)=-1-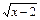 x∈[2,3] …………4分
x∈[2,3] …………4分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



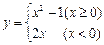
 的最小值为
的最小值为


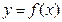 的反函数为
的反函数为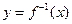 ,且
,且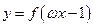 的图象过点
的图象过点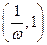 ,则
,则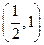



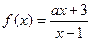 的反函数为
的反函数为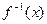 ,若函数
,若函数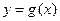 的图象与函数
的图象与函数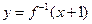 的图象关于直线
的图象关于直线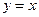 对称,且
对称,且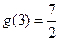 ,则实数
,则实数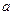 的值为
的值为 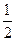
 的反函数是( )
的反函数是( )




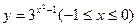 的反函数是
的反函数是