网址:http://m.1010jiajiao.com/timu_id_192743[举报]
(本题满分12分)探究函数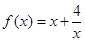 ,
, 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时 的值,列表如下:
的值,列表如下:
|
|
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
|
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中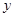 值随
值随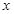 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当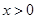 时,
时,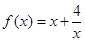 在区间
在区间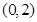 上递减,在区间 上递增;
上递减,在区间 上递增;
所以,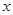 =
时,
=
时, 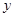 取到最小值为
;
取到最小值为
;
(2) 由此可推断,当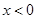 时,
时,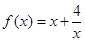 有最
值为 ,此时
有最
值为 ,此时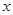 =
;
=
;
(3) 证明: 函数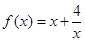 在区间
在区间 上递减;
上递减;
(4) 若方程 在
在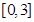 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数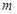 的取值范围。
的取值范围。
查看习题详情和答案>>
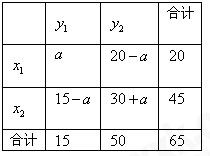
若某产品的直径长与标准值的差的绝对值不超过1mm 时,则视为合格品,否则视为不合格品。在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品。计算这50件不合格品的直径长与标准值的差(单位:mm), 将所得数据分组,得到如下频率分布表:
|
分组 |
频数 |
频率 |
|
[-3, -2) |
|
0.10 |
|
[-2, -1) |
8 |
|
|
(1,2] |
|
0.50 |
|
(2,3] |
10 |
|
|
(3,4] |
|
|
|
合计 |
50 |
1.00 |
(Ⅰ)将上面表格中缺少的数据填在答题卡的相应位置;
(Ⅱ)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(Ⅲ)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
【解析】(Ⅰ)
|
分组 |
频数 |
频率 |
|
[-3, -2) |
5 |
0.10 |
|
[-2, -1) |
8 |
0.16 |
|
(1,2] |
25 |
0.50 |
|
(2,3] |
10 |
0.2 |
|
(3,4] |
2 |
0.04 |
|
合计 |
50 |
1.00 |
(Ⅱ)根据频率分布表可知,落在区间(1,3]内频数为35,故所求概率为0.7.
(Ⅲ)由题可知不合格的概率为 0.01,故可求得这批产品总共有2000,故合格的产品有1980件。
0.01,故可求得这批产品总共有2000,故合格的产品有1980件。
查看习题详情和答案>>
(本题满分12分)探究函数![]() ,
,![]() 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时![]() 的值,列表如下:
的值,列表如下:
|
| … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
|
| … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中![]() 值随
值随![]() 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当![]() 时,
时,![]() 在区间
在区间![]() 上递减,在区间 上递增;
上递减,在区间 上递增;
所以,![]() = 时,
= 时, ![]() 取到最小值为 ;
取到最小值为 ;
(2) 由此可推断,当![]() 时,
时,![]() 有最 值为 ,此时
有最 值为 ,此时![]() = ;
= ;
(3) 证明: 函数![]() 在区间
在区间![]() 上递减;
上递减;
(4) 若方程![]() 在
在![]() 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数![]() 的取值范围。
的取值范围。
查看习题详情和答案>>
 ,x∈(0,+∞)的最小值,并确定取得最小值时x的值,列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值,列表如下: 
 在区间(0,2)上递减,在区间______上递增;所以,x=______时,y取到最小值为______;
在区间(0,2)上递减,在区间______上递增;所以,x=______时,y取到最小值为______; 有最______值为______,此时x=______;
有最______值为______,此时x=______;  在区间(0,2)上递减;
在区间(0,2)上递减;