网址:http://m.1010jiajiao.com/timu_id_192514[举报]
(本题满分18分,第(1)小题6分,第(2)小题6分,第(3)小题6分)
若数列![]() 满足:
满足:![]() 是常数),则称数列
是常数),则称数列![]() 为二阶线性递推数列,且定义方程
为二阶线性递推数列,且定义方程![]() 为数列
为数列![]() 的特征方程,方程的根称为特征根; 数列
的特征方程,方程的根称为特征根; 数列![]() 的通项公式
的通项公式![]() 均可用特征根求得:
均可用特征根求得:
①若方程![]() 有两相异实根
有两相异实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
②若方程![]() 有两相同实根
有两相同实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
再利用![]() 可求得
可求得![]() ,进而求得
,进而求得![]() .
.
根据上述结论求下列问题:
(1)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(2)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(3)当![]() ,
,![]() (
(![]() )时,记
)时,记![]() ,若
,若![]() 能被数
能被数![]() 整除,求所有满足条件的正整数
整除,求所有满足条件的正整数![]() 的取值集合.
的取值集合.
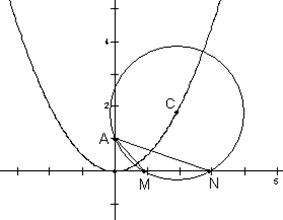
(本题满分16分)已知:圆C过定点A(0,p),圆心C在抛物线x2=2py上运动,若MN为圆C在X轴上截和的弦,设|AM|=m,|AN|=n,∠MAN=α,
(1).当点C运动时,|MN|是否变化?写出并证明你的结论;
(2).求![]() 的最大值,并求取得这个最大值时α的值和此时圆C的方程.
的最大值,并求取得这个最大值时α的值和此时圆C的方程.
 |
(本题满分16分)已知:圆C过定点A(0,p),圆心C在抛物线x2=2py上运动,若MN为圆C在X轴上截和的弦,设|AM|=m,|AN|=n,∠MAN=α,
(1).当点C运动时,|MN|是否变化?写出并证明你的结论;
(2).求![]() 的最大值,并求取得这个最大值时α的值和此时圆C的方程.
的最大值,并求取得这个最大值时α的值和此时圆C的方程.
 |
若数列
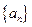 满足:
满足: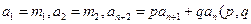 是常数),则称数列
是常数),则称数列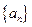 为二阶线性递推数列,且定义方程
为二阶线性递推数列,且定义方程 为数列
为数列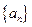 的特征方程,方程的根称为特征根; 数列
的特征方程,方程的根称为特征根; 数列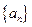 的通项公式
的通项公式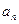 均可用特征根求得:
均可用特征根求得:①若方程
 有两相异实根
有两相异实根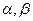 ,则数列通项可以写成
,则数列通项可以写成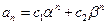 ,(其中
,(其中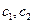 是待定常数);
是待定常数);②若方程
 有两相同实根
有两相同实根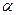 ,则数列通项可以写成
,则数列通项可以写成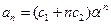 ,(其中
,(其中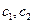 是待定常数);
是待定常数);再利用
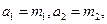 可求得
可求得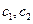 ,进而求得
,进而求得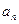 .
.根据上述结论求下列问题:
(1)当
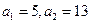 ,
,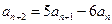 (
(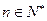 )时,求数列
)时,求数列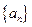 的通项公式;
的通项公式;(2)当
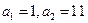 ,
,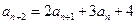 (
(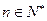 )时,求数列
)时,求数列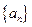 的通项公式;
的通项公式;(3)当
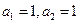 ,
,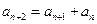 (
(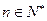 )时,记
)时,记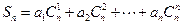 ,若
,若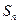 能被数
能被数 整除,求所有满足条件的正整数
整除,求所有满足条件的正整数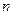 的取值集合.
的取值集合.已知函数 ,
, .
.
(Ⅰ)若函数 和函数
和函数 在区间
在区间 上均为增函数,求实数
上均为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 有唯一解,求实数
有唯一解,求实数 的值.
的值.
【解析】第一问, 
当0<x<2时, ,当x>2时,
,当x>2时, ,
,
要使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须

如使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须 ,即
,即
由上得出,当 时
时 ,
, 在
在 上均为增函数
上均为增函数
(Ⅱ)中方程 有唯一解
有唯一解 有唯一解
有唯一解
设 (x>0)
(x>0)
 随x变化如下表
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为-24-16ln2,
的最小值为-24-16ln2,
当m=-24-16ln2时,方程 有唯一解得到结论。
有唯一解得到结论。
(Ⅰ)解:
当0<x<2时, ,当x>2时,
,当x>2时, ,
,
要使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须

如使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须 ,即
,即
由上得出,当 时
时 ,
, 在
在 上均为增函数 ……………6分
上均为增函数 ……………6分
(Ⅱ)方程 有唯一解
有唯一解 有唯一解
有唯一解
设 (x>0)
(x>0)
 随x变化如下表
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为-24-16ln2,
的最小值为-24-16ln2,
当m=-24-16ln2时,方程 有唯一解
有唯一解
查看习题详情和答案>>






