题目内容
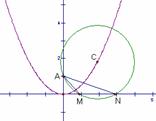
（本题满分16分）已知：圆C过定点A(0，p)，圆心C在抛物线x2=2py上运动，若MN为圆C在X轴上截和的弦，设|AM|=m，|AN|=n，∠MAN=α,
(1).当点C运动时，|MN|是否变化？写出并证明你的结论；
(2).求
的最大值，并求取得这个最大值时α的值和此时圆C的方程.
 |
(1)解法一：过C作CH⊥x轴于H
设C(x0,
)
∴MN=2MH=
.
解法二：由题意得：⊙C的方程(x-x0)2+(y-y0)2=x02+(y0-1)2.
把y=0和x02=2py0代入整理得x2-2x0x+x02+xp2=0. 解之得方程的两根分为
x1=x0-p，x2=x0+p. ∴ |MN|=|x1-x2|=2P.
∴点C运动时，|MN|不会变化，|MN|=2P(定值)
(2)设∠MAN=
∵
|OA||MN|=p2，∴
∵
， ∴
.
∴
.
∵只有当C在O点处时，为直径上圆周角，其他时候都是劣弧上的圆周角.
∴
，
故当
时，原式有最大值
.
∵∠MAN=
，∴∠MCN=2∠MAN=
∴y0=P，x0=
，r=
.
所求圆的方程为
练习册系列答案
阅读快车系列答案
相关题目
，且对任意
，有
.
；
在区间（0，1）上为单调函数，求实
数
的取值范围.
的零点个数？(提示
)
为实常数）．
时，求函数
在
上的最小值；
在区间
上有解，求实数
的取值范围；
）
：
的离心率为
，
分别为椭圆
为椭圆上任意一点，以
为半径作圆
有公共点时，求△
面积的最大值．
是定义在
上的偶函数，且当
时，
。
及
的值；
上的解析式；
的方程
有四个不同的实数解，求实数
的取值范围。